JOISC 2023 做题记录

Day 1

A. Two Currencies

贪心选链上最小的几个收费站用银币付，显然是对的．

使用主席树加速贪心，复杂度 $O(n \log n)$．

注意一条边上可能有多个收费站．

* B. Festivals in JOI Kingdom 2

我是计数菜逼．/ll

首先，正确的贪心应该是将区间按照右端点升序排序贪心．下文中称正确的贪心为算法 A，假贪心为算法 B．然后再称被算法 A 选中的区间为 A 区间，被算法 B 选中的区间为 B 区间，不会被任何算法选中的区间为 F 区间．

这个时候是不是应该观察一下性质！设我们有 $n$ 个区间 $[l_1, r_1], [l_2, r_2], \cdots [l_n, r_n]$，A 区间的下标序列为 $a_1, a_2, \cdots, a_p$，B 区间的下标序列为 $b_1, b_2, \cdots, b_q$，由于我们的贪心是对的，所以有 $p \ge q$．

先来看算法 A，由于算法 A 按右端点升序贪心，可以观察到：

1. 不存在 $i$，使得 $r_i < r_{a_1}$．
2. 不存在 $i, j$，使得 $r_{a_j} < l_i$ 且 $r_i < r_{a_{j + 1}}$．

对于算法 B，类似地有：

1. 不存在 $i$，使得 $l_i < l_{b_1}$．
2. 不存在 $i, j$，使得 $r_{b_j} < l_i$ 且 $l_i < l_{b_{j + 1}}$．

显然，这是充要的．

然后我们尝试解决这个计数问题，发现直接计数很难，但是总方案数是可以算的，所以应当计算 $p = q$ 的方案数．

这时候需要巨量观察，我先从官方题解中贺一张图：

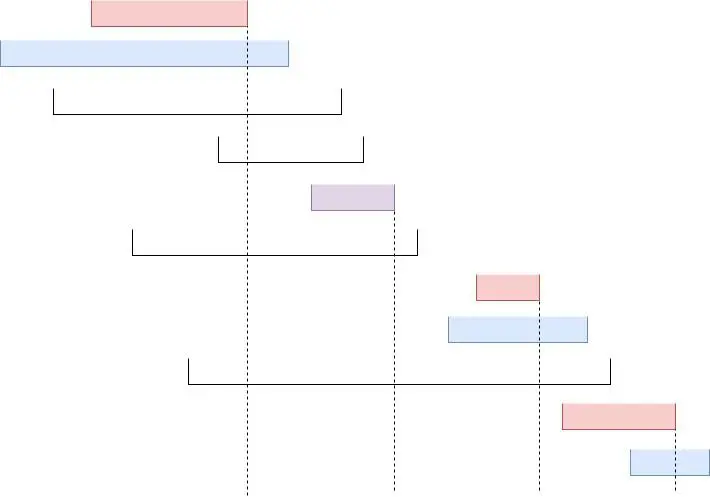
其中红色区间为 A 区间，蓝色区间为 B 区间，紫色区间同时为 A 区间和 B 区间，未被染色的区间为 F 区间．

可以发现，在某个 $p = q$ 的选择方案中：

1. $l_{b_1} \le l_{a_1}$，$r_{a_1} \le r_{b_1}$．否则不满足两个算法的条件 1．
2. $r_{a_i} \le r_{b_i}$．否则不满足算法 A 的条件 2．
3. $[l_{a_i}, r_{a_i}] \cap [l_{b_i}, r_{b_i}] \not= \varnothing$．否则 $[l_{b_i}, r_{b_i}]$ 会被算法 A 选中，此时不满足 $p = q$．
4. $r_{b_{i - 1}} < r_{a_i}$，否则由于 $r_{b_{i - 1}} < l_{b_i}$，不满足条件 3.

然后就可以开始设计 DP 了！我们大概需要设计一个这样的东西：每次插入一对 A、B 区间和若干 F 区间，然后在这一过程中计算方案数．

然后我们发现，如果我们按照两算法的选择顺序插入区间，为了满足上述所有条件，F 区间能够选择的左端点数会和前面的具体放置方案相关，必须要设计到状态里，做出一个类似线头 DP 的东西．但是 F 区间的右端点限制是非常松的：只需要在当前 A 区间右端点的右边．这启发我们倒序插入区间．

设 $f_{i, 0 / 1}$ 表示插入了后 $i$ 个区间，上次插入的 A、B 区间是否不同的方案数．转移枚举插 $j$ 个 F 区间，使得这 $j$ 个 F 区间的左端点在当前插入的 A 区间的右端点右边，分类讨论：

1. $f_{i, 1} \to f_{i + j + 2, 1}$．

   此时要分两类讨论：

   1. 当前插入的 B 区间右端点在上一次插入的 A 区间左端点的左边，如图：

      

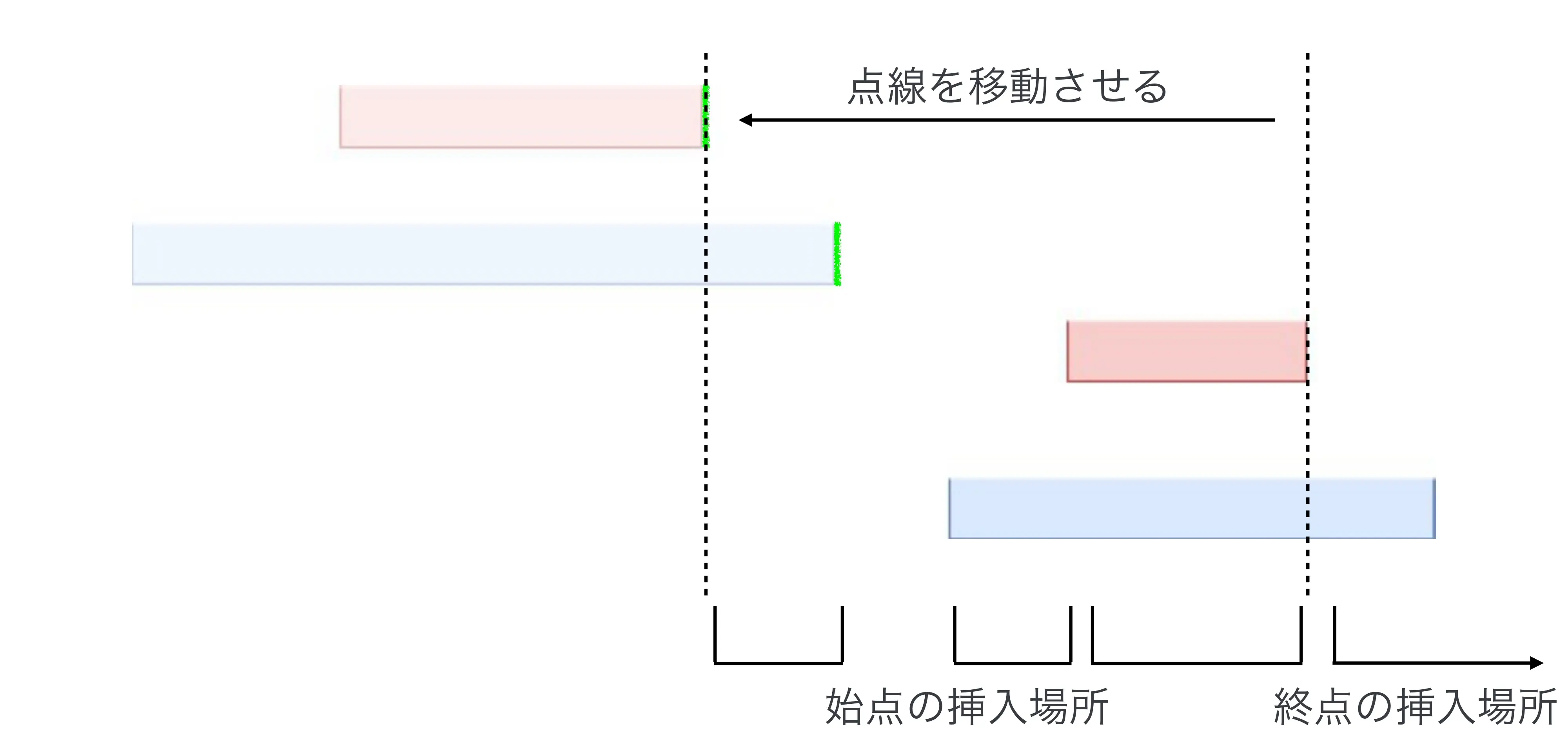
      考虑 F 区间右端点的方案数：考虑逐个插入右端点，对于第 $1$ 个插入的右端点，如图所示，可插入的范围中一共有 $2(i - 2) + 1$ 个点，也就是有 $2(i - 2) + 1 + 1 = 2i - 2$ 个区间可供插入，而插入后又会新增一个区间，故插入一共 $j$ 个右端点的方案数为 $(2i - 2)^{\overline{j}}$．

      再考虑安排 F 区间的左端点：由于右端点已经标号，所以左端点直接按序匹配就能不重不漏地统计所有方案，不用再次标号，而又由于 B 区间的条件 2，相邻 B 区间之间不能有左端点，那么方案数就相当于把 $j$ 个球放入 $3$ 个盒子中，盒子可空，即为 $\binom{j + 3 - 1}{3 - 1} = \binom{j + 2}{2}$．

      于是得到这种情况的转移：$f_{i, 1} \times \binom{j + 2}{2} \times (2i - 2)^{\overline{j}} \to f_{i + j + 2, 1}$

   2. 当前插入的 B 区间右端点在上一次插入的 A 区间左端点的右边，如图：

      

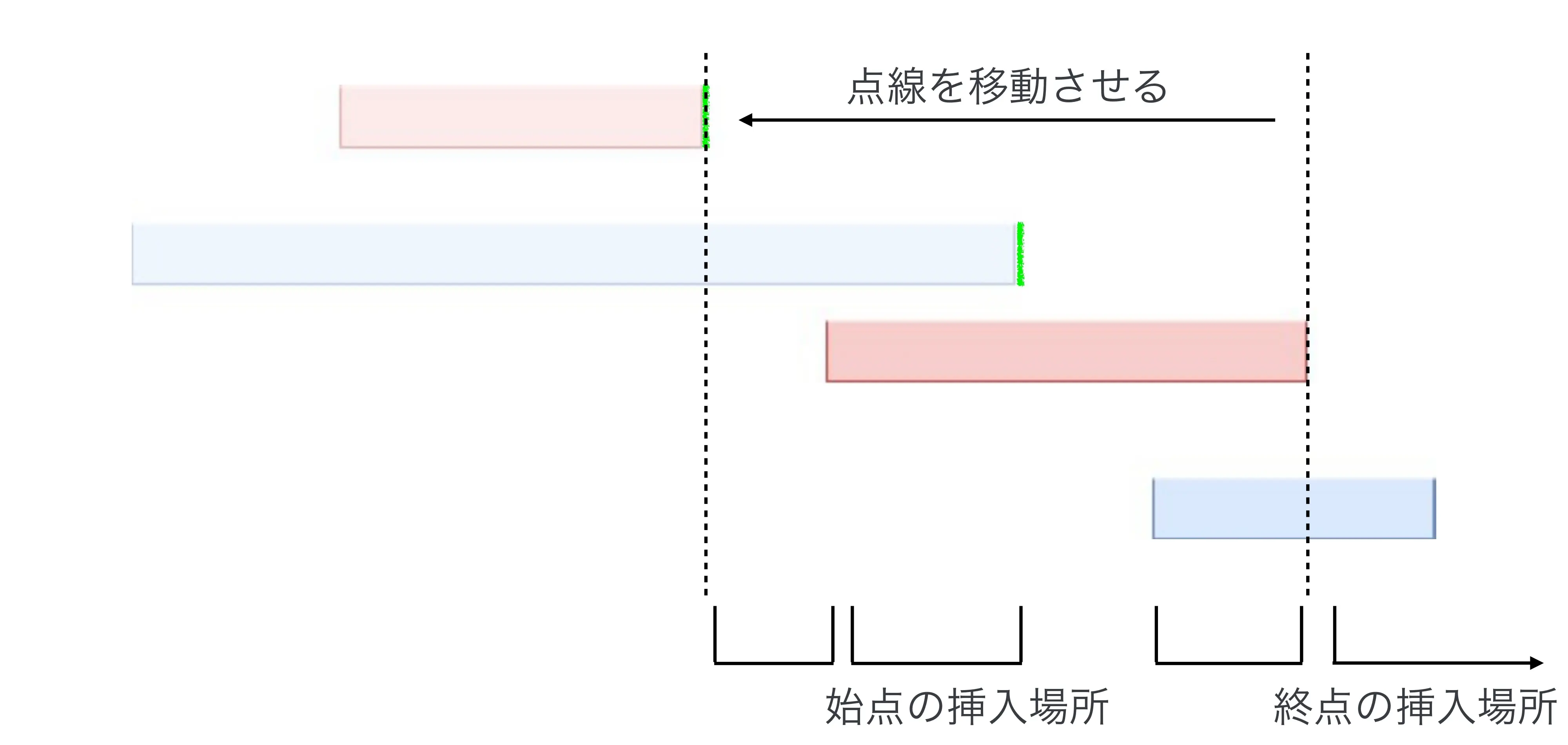
      发现转移和上面那种情况是一样的，可以直接合到一起转移！

   于是得到这种情况的转移方程：

   $$f_{i, 1} \times (j + 2)^{\underline{2}} \times (2i - 2)^{\overline{j}} \to f_{i + j + 2, 1}$$

2. $f_{i, 1} \to f_{i + j + 1, 0}$．

   转移和 1 情况的差别只有左端点能够选择的区间数目变成了 $2$，故转移方程为：

   $$f_{i, 1} \times (j + 1) \times (2i - 2)^{\overline{j}} \to f_{i + j + 1, 0}$$

3. $f_{i, 0} \to f_{i + j + 2, 1}$．

   此时左端点只有 $2$ 个区间可选，且右端点能选择的区间内只有 $2(i - 1) = 2i - 2$ 个端点，故转移方程为：

   $$f_{i, 0} \times (j + 1) \times (2i - 1)^{\overline{j}} \to f_{i + j + 2, 1}$$

4. $f_{i, 0} \to f_{i + j + 1, 0}$．

   左端点只有 $1$ 个区间可选，且右端点能选择的区间内只有 $2i - 2$ 个端点，故转移方程为：

   $$f_{i, 0} \times (2i - 1)^{\overline{j}} \to f_{i + j + 1, 0}$$

然后发现还有 F 区间左端点在第一个 A 区间右端点左边的方案没有统计，类似讨论即可．

时间复杂度 $O(n ^ 2)$，在 loj 上能过．正解还要上个半在线卷积．

* C. Passport

可以注意到，由于签发国家总是被对应的可达区间包含，于是可达所有点等价于可达 $1$ 和 $n$．

如果只用到达一边可以直接线段树优化建边跑最短路解决，但是现在要求到达两边的最小代价．有一个朴素的想法是，对点 $i$ 分别求出到 $1$ 的代价 $c_{1, i}$ 和到 $n$ 的代价 $c_{n, i}$，然后答案就是 $c_{1, i} + c_{n, i}$．这显然是错的，因为两段路径可能有交．

然后就不会了啊！看题解发现最优方案一定形如起点先到达某个中继点，然后再从中继点前往 $1$ 和 $n$，然后就先将每一个点的答案初始化成 $c_{1, i} + c_{n, i}$，再跑一遍 01 bfs 松弛掉重复的部分．

Day 2

! A. Belt Conveyor

交互．以后再补．

B. Council

考虑如何求 $i$ 的答案，先将 $i$ 扣掉，此时支持人数 $< \lfloor n / 2 \rfloor$ 的议案已经寄了，$> \lfloor n / 2 \rfloor$ 的议案肯定能选到，于是只用考虑选取副议长对支持人数 $= \lfloor n / 2 \rfloor$ 的议案的影响．设 $S_i$ 表示 $i$ 不支持 的议案的集合，$T$ 表示当前支持人数 $= \lfloor n / 2 \rfloor$ 的议案的集合，我们要求的就是 $\max\limits_{j \not= i} |T \cap S_j|$．

这个可以两遍高维前缀和解决：先将每个 $S$ 贡献到它的子集上，标记哪些子集是能产生的，然后再将这些子集大小贡献到它的超集上．注意由于有 $j \not= i$ 的限制，需要记录来源不同的最大和次大子集大小．

* C. Mizuyokan 2

好牛逼．

首先发现，对于合法的一个划分，一定能够通过调整划分方案，使得作为谷的连续段长度为 $1$．

然后可以发现，如果我们划分出了若干段 $[l_i, r_i]$，使得对于所有 $i$，有 $\sum\limits_{j = l_i}^{r_i} a_i > \max\{a_{l_i - 1}, a_{r_i + 1}\}$，那么一定可以在此基础上调整出一个满足题意方案．显然这种划分和题目中给定的划分等价，拥有同样的段数上界．

下文中称将一个数选出来作为某个 $r_i + 1$ 为选择这个数．由于要划分出尽量多的段，所以我们希望下一个选中的位置距离当前位置尽量近．设 $\mathrm{nxt}_i$ 为下一个选择的位置，再记 $\mathrm{pre}_i$ 为最大的 $j$，使得 $\sum\limits_{k = j + 1}^{i - 1} a_k > \max\{a_j, a_i\}$，那么 $\mathrm{nxt}_i$ 就是最小的 $j$，使得 $\mathrm{pre}_j \ge i$．求出 $\mathrm{nxt}$ 后倍增就能过掉不带修改的包．

考虑带修改怎么做，这个时候有牛逼结论：

引理 1：$\mathrm{nxt}_i - i$ 是 $O(\log V)$ 级别的．

证明：

令 $c = i + \lfloor \log V \rfloor + 2$．考虑反证法，令该结论不成立，那么对于所有 $i \le j < c$，都有 $a_j \le \sum\limits_{k = j + 1}^{c - 1} a_k$，归纳一下可以得出，$a_i \ge 2^{c - 1 - i} a_c \ge 2^{c - 1 - i} \ge 2^{\lfloor \log V \rfloor + 1} > V$，矛盾．

然后就可以在线段树上维护每个区间前 $O(\log V)$ 个位置在区间内能够跳到的最远位置和步数．每次修改暴力重算有用的 $\mathrm{pre}$ 和 $\mathrm{nxt}$ 后重建线段树即可．时间复杂度 $O(n \log n \log V)$．

Day 3

* A. Chorus

感谢 这篇题解，感觉比官方题解更清晰！

将 A 看作 $\texttt{(}$，B 看作 $\texttt{)}$，题意就是经过最小次数的交换，使得能够划分出 $k$ 个子序列，让每个子序列都形如 $\texttt{(((} \cdots \texttt{)))}$．

然后不会做了！看题解得知，无论如何划分，第 $i$ 个 A 和第 $i$ 个 B 一定匹配．也就是说，如果我们让第 $l$ 个到第 $r$ 个 A 在一个子序列中，那么第 $l$ 个到第 $r$ 个 B 也要再这一子序列中，且能够匹配也就是说必须被移动到第 $r$ 个 A 后面．

设 $\mathrm{ct}_i$ 为第 $i$ 个 A 前有多少个 B，那么划分出第 $l$ 个到第 $r$ 个 A 造成的代价就是 $\sum\limits_{i = l}^r \max\{\mathrm{ct}_i - (l - 1), 0\}$．

然后就可以 DP 了！设 $f_{i, j}$ 表示前 $i$ 个 A 划分出 $j$ 段的最小代价，转移枚举上次划分在那里，容易做到 $O(n^3)$．然后发现这个代价函数满足四边形不等式，整个问题就是凸的了！wqs 二分套个斜率优化即可．

* B. Cookies

引理 1：对于选出的一组盒子，设将其大小从大到小排列后的序列为 $b$，那么这组选法合法当且仅当对于所有 $i$，有 $\sum\limits_{j = 1}^i c_j \le \sum_{j = 1}^n \min\{i, a_j\}$．

我不会证，但是可以感受！

于是可以设 $f_{i, j, k}$ 表示选了前 $i$ 个盒子，考虑了大于 $j$ 的所有盒子，当前方案和为 $k$．转移就是 $f_{i, j + 1, k} \to f_{i, j, k}$ 和 $f_{i - 1, j, k - j} \to f_{i, j, k}$．

$k$ 那一维使用 bitset 优化转移．

C. Tourism

套路世界大战！

可以求出区间内每一个点到根节点的路径并大小，然后减去区间 LCA 到根的路径大小，就是区间虚树覆盖的点集大小．

区间 LCA 可以通过查询区间 dfn 最小值和最大值，求它们对应点的 LCA 解决；路径并大小是经典套路，拿一个 LCT 然后扫描线，access 一下新加的点，每次虚实边切换时撤销上次的贡献并插入当前的贡献，复杂度 $O(n \log^2 n)$．

Day 4

! A. The Last Battle

通信．以后再补．

! B. Security Guard

看不懂题，摆了．

C. Bitaro’s Travel

首先已经到达过的点一定是一段连续的区间，然后每次转向时，这个区间长度至少翻倍．

模拟转向即可．转向点可以二分．