注意到
a i b j + a j b k + a k b i ≥ a k b j + a j b i + a i b k ⟺ ( a k − a j ) ( b i − b j ) − ( a i − a j ) ( b k − b j ) ≥ 0 a_i b_j+a_j b_k+a_k b_i \ge a_k b_j+a_j b_i+a_i b_k \iff (a_k - a_j)(b_i - b_j) - (a_i - a_j)(b_k - b_j) \ge 0
a i b j + a j b k + a k b i ≥ a k b j + a j b i + a i b k ⟺ ( a k − a j ) ( b i − b j ) − ( a i − a j ) ( b k − b j ) ≥ 0
故若令 A i = ( a i , b i ) A_i = (a_i, b_i) A i = ( a i , b i ) A i A i + 1 → × A i + 1 A i + 2 → ≥ 0 \overrightarrow{A_iA_{i + 1}} \times \overrightarrow{A_{i + 1}A_{i + 2}} \ge 0 A i A i + 1 × A i + 1 A i + 2 ≥ 0
唐.
不妨枚举 a , b a, b a , b p , q p, q p , q a i ≤ p a_i \le p a i ≤ p b i ≤ q b_i \le q b i ≤ q p p p q q q max c i + max d i + q \max c_i + \max d_i + q max c i + max d i + q max \max max max \max max
还没补.
我们选取一个联通块中最小的且最靠左上方的元素作为这个连通块的特征元素,对联通块计数即对特征元素计数.
考虑一个元素 ( i , j ) (i, j) ( i , j ) ( i , j ) → ( i , k ) → ( p , k ) → ( p , j ) (i, j) \to (i, k) \to (p, k) \to (p, j) ( i , j ) → ( i , k ) → ( p , k ) → ( p , j ) b k < b j b_k < b_j b k < b j a i + b k < a i + b j a_i + b_k < a_i + b_j a i + b k < a i + b j w i , k < w i , j w_{i, k} < w_{i, j} w i , k < w i , j
故设 p a i \mathrm{pa}_i p a i j j j a j < a i a_j < a_i a j < a i s a i \mathrm{sa}_i s a i j j j a j < a i a_j < a_i a j < a i p b i , s b i \mathrm{pb}_i, \mathrm{sb}_i p b i , s b i ( i , j ) (i, j) ( i , j )
a i + b j ≤ x a i + min { max k = p b j j b k , max k = j s b j b k } > x b j + min { max k = p a i i a k , max k = i s a i a k } > x \begin{aligned}
a_i + b_j \le x \\
a_i + \min\{\max_{k = \mathrm{pb}_j}^{j} b_k, \max_{k = j}^{\mathrm{sb}_j} b_k\} > x \\
b_j + \min\{\max_{k = \mathrm{pa}_i}^{i} a_k, \max_{k = i}^{\mathrm{sa}_i} a_k\} > x
\end{aligned}
a i + b j ≤ x a i + min { k = p b j max j b k , k = j max s b j b k } > x b j + min { k = p a i max i a k , k = i max s a i a k } > x
扫描线即可.
假设我们设定了阈值 x x x a i y < x , b j y > x a_i^y < x, b_j^y > x a i y < x , b j y > x y y y O ( n log n ) O(n \log n) O ( n log n )
然后扫描线即可.
分类讨论.
m = n m = n m = n
m = 2 m = 2 m = 2
m = 3 m = 3 m = 3 T 1 > T 2 T_1 > T_2 T 1 > T 2 T 2 > T 3 T_2 > T_3 T 2 > T 3
T 1 > T 2 T_1 > T_2 T 1 > T 2 ∣ T 2 ∣ = 1 |T_2| = 1 ∣ T 2 ∣ = 1
T 2 > T 3 T_2 > T_3 T 2 > T 3
T 2 T_2 T 2 T 3 T3 T 3 ∣ T 2 ∣ = 1 |T_2| = 1 ∣ T 2 ∣ = 1 剩下的情况,T 2 T_2 T 2 ∣ T 2 ∣ |T_2| ∣ T 2 ∣
于是直接枚举连续段作为 T 2 T_2 T 2
m ≥ 4 m \ge 4 m ≥ 4 i i i s i > s i + 1 s_i > s_{i + 1} s i > s i + 1 s i = s i + 1 = s i + 2 s_i = s_{i + 1} = s_{i + 2} s i = s i + 1 = s i + 2
一种作物分布唯一对应一个最小的能够将所有有作物的格子框住的矩形,我们称这个矩形为这个分布的特征矩形.
考虑枚举矩形,计算特征矩形为当前矩形的分布个数.需要很麻烦的分讨.咕咕咕咕.
还没补.
还没补.
没打.
回想到对于一个序列 a i a_i a i k k k P ( x ) P(x) P ( x ) P ( i ) = a i P(i) = a_i P ( i ) = a i a a a k + 1 k + 1 k + 1 0 0 0
故只用找到 b b b k + 1 k + 1 k + 1 a a a k + 1 k + 1 k + 1
考查 k + 1 k + 1 k + 1
Δ n a i = ∑ j ( k + 1 j ) ( − 1 ) k + 1 − j a i + j \Delta^n a_i = \sum_j \binom{k + 1}{j} (-1)^{k + 1 - j} a_{i + j}
Δ n a i = j ∑ ( j k + 1 ) ( − 1 ) k + 1 − j a i + j
是一个卷积的形式,直接 FFT 加速卷积即可.
没写完代码. \Huge\color{red}\text{没写完代码.} 没写完代码.
记 [ l , r ] [l, r] [ l , r ] m m m S l , r S_{l, r} S l , r r r r r e s r , l \mathrm{res}_{r, l} r e s r , l S l , r S_{l, r} S l , r r e s r − 1 \mathrm{res}_{r - 1} r e s r − 1 r e s r \mathrm{res}_{r} r e s r
考虑维护一个类单调栈的结构,具体地,对于一个 r r r S l , r ≠ S l + 1 , r S_{l, r} \not= S_{l + 1, r} S l , r = S l + 1 , r l l l ≥ m \ge m ≥ m ≥ \ge ≥ m m m O ( n m ) O(nm) O ( n m )
但是每次插入都会遍历一次这个链表,这一部分复杂度是 O ( n 2 ) O(n^2) O ( n 2 ) m m m ≥ \ge ≥ O ( n m ) O(nm) O ( n m )
有了关键点的链表,维护 r e s r \mathrm{res}_r r e s r 你猜猜我为啥没写完代码 .
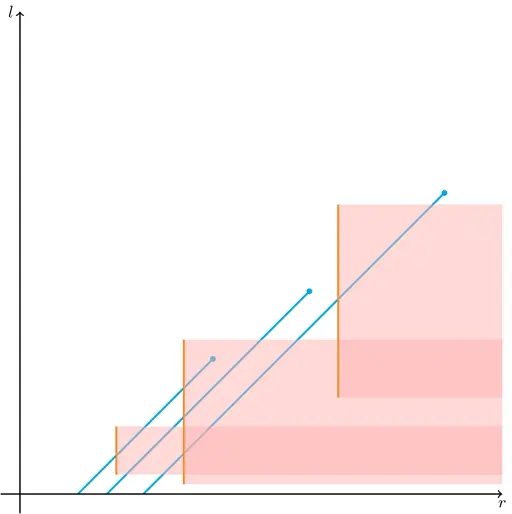
显然上述的维护过程会造成一车区间加,而答案可写作下式:
∑ r − l + 1 = x r e s r , l \sum_{r - l + 1 = x} \mathrm{res}_{r, l}
r − l + 1 = x ∑ r e s r , l
是一个斜 45 度的历史和的形式,如下图
图中橙色竖线代表一次区间加,红色矩形代表这次区间加的影响范围,青色点代表一个询问点,青色斜线代表这次询问需要统计的贡献范围.
首先先将 3-side 矩形加差分成 2-side 矩形加,然后我们可以将每个 2-side 矩形加记作三元组 ( s i , t i , d i ) (s_i, t_i, d_i) ( s i , t i , d i ) ( s i , t i ) (s_i, t_i) ( s i , t i ) ( p , q ) (p, q) ( p , q )
∑ t i ≤ q ( q − t i + 1 ) d i + ∑ p − s i ≤ q − t i ( ( p − s i + 1 ) − ( q − t i + 1 ) ) d i = ( q + 1 ) ∑ t i ≤ q d i − ∑ t i ≤ q t i d i + ( p − q ) ∑ p − q ≤ s i − t i d i − ( s i − t i ) ∑ p − q ≤ s i − t i t i d i \begin{aligned}
& \sum_{t_i \le q} (q - t_i + 1) d_i + \sum_{p - s_i \le q - t_i} ((p - s_i + 1) - (q - t_i + 1)) d_i \\
=\ & (q + 1) \sum_{t_i \le q} d_i - \sum_{t_i \le q} t_i d_i + (p - q) \sum_{p - q \le s_i - t_i} d_i - (s_i - t_i) \sum_{p - q \le s_i - t_i} t_i d_i
\end{aligned}
= t i ≤ q ∑ ( q − t i + 1 ) d i + p − s i ≤ q − t i ∑ ( ( p − s i + 1 ) − ( q − t i + 1 ) ) d i ( q + 1 ) t i ≤ q ∑ d i − t i ≤ q ∑ t i d i + ( p − q ) p − q ≤ s i − t i ∑ d i − ( s i − t i ) p − q ≤ s i − t i ∑ t i d i
故只需支持单点加查询前缀和.又我们有 O ( n m ) O(nm) O ( n m ) O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 ) O ( n ) O(\sqrt{n}) O ( n ) O ( n m ) O(nm) O ( n m )
若我们预处理出了 f i , j f_{i, j} f i , j ( 1 , 1 ) (1, 1) ( 1 , 1 ) ( i , j ) (i, j) ( i , j ) g i , j g_{i, j} g i , j ( R , C ) (R, C) ( R , C ) ( i , j ) (i, j) ( i , j )
若 Bob 的路径已经确定,那么可以通过尝试拼接路径两侧的 f f f g g g
具体地,设 h i , j , 0 / 1 h_{i, j, 0 / 1} h i , j , 0 / 1 ( 1 , C ) (1, C) ( 1 , C ) ( i , j ) (i, j) ( i , j )
shaber 点分治题.
考虑计算跨越一个点 r r r r r r r r r ∞ \infty ∞ u p u \mathrm{up}_u u p u u p u \mathrm{up}_u u p u r e m u \mathrm{rem}_u r e m u ≤ r e m u \le \mathrm{rem}_u ≤ r e m u u u u r r r
r e m v ← min { r e m u − d v , k v } \mathrm{rem}_v \leftarrow \min\{\mathrm{rem}_u - d_v, k_v\}
r e m v ← min { r e m u − d v , k v }
若当前在 u u u v v v d v ≤ r e m u d_v \le \mathrm{rem}_u d v ≤ r e m u
再记 d n u \mathrm{dn}_u d n u ≤ d n u \le \mathrm{dn}_u ≤ d n u r r r u u u d n u \mathrm{dn}_u d n u s u s_u s u r r r u u u r r r
d n v ← min { d n u , k v − s u m u } \mathrm{dn}_v \leftarrow \min\{\mathrm{dn}_u, k_v - \mathrm{sum}_u\}
d n v ← min { d n u , k v − s u m u }
那么相当于统计满足 a u ≤ a v a_u \le a_v a u ≤ a v u p u ≤ d n v \mathrm{up}_u \le \mathrm{dn}_v u p u ≤ d n v ( u , v ) (u, v) ( u , v ) O ( n log 2 n ) O(n \log^2 n) O ( n log 2 n )
还没补.
注意到幂塔只有前 30 个位置有用,故倒着 DP,转移只枚举前 30 个位置,后面的直接前缀和计算.
然后这 b 题卡常,注意到计算幂塔的模数除开前三个(分别为 998244353 , 998244352 , 402653184 998244353, 998244352, 402653184 9 9 8 2 4 4 3 5 3 , 9 9 8 2 4 4 3 5 2 , 4 0 2 6 5 3 1 8 4 2 2 2 O ( n log 3 V ) O(n \log^3 V) O ( n log 3 V )
考虑对每个左端点 i i i f i f_i f i [ i , f i ] [i, f_i] [ i , f i ] ∑ n − f i + 1 \sum n - f_i + 1 ∑ n − f i + 1
注意到 b i > a i b_i > a_i b i > a i f i f_i f i [ p l , p r ] [\mathrm{pl}, \mathrm{pr}] [ p l , p r ] f f f [ l , r ] [l, r] [ l , r ] p m i d = ⌊ ( p l + p r ) / 2 ⌋ \mathrm{pmid} = \lfloor (\mathrm{pl} + \mathrm{pr}) / 2 \rfloor p m i d = ⌊ ( p l + p r ) / 2 ⌋ [ l , r ] [l, r] [ l , r ] i i i [ i , p m i d ] [i, \mathrm{pmid}] [ i , p m i d ] f f f
复杂度貌似是 O ( n V log n ) O(nV \log n) O ( n V log n )
垃圾东西.注意到字母对很少,考虑将询问离线,逐一计算每一对字母对询问的贡献.
对于字母对 ( c 1 , c 2 ) (c_1, c_2) ( c 1 , c 2 ) c 1 c_1 c 1 c 2 c_2 c 2 c 1 c_1 c 1 1 1 1 c 2 c_2 c 2 0 0 0 ( n ∣ Σ ∣ + m ∣ Σ ∣ 2 ) (n|\Sigma| + m|\Sigma|^2) ( n ∣ Σ ∣ + m ∣ Σ ∣ 2 )
记数字 i i i c t i \mathrm{ct}_i c t i p p p
⌊ ∑ i min { c t i , c t p − i } 2 ⌋ \left\lfloor \frac{\sum_{i} \min\{\mathrm{ct}_i, \mathrm{ct}_{p - i}\}}{2} \right\rfloor
⌊ 2 ∑ i min { c t i , c t p − i } ⌋
考虑如何计算分子,发现是个卷积的形式.又注意到 c t i \mathrm{ct}_i c t i O ( n ) O(\sqrt{n}) O ( n ) x x x c t i = x \mathrm{ct}_i = x c t i = x i i i
∑ x ∑ i [ c t i = x ] [ c t p − i ≤ x ] c t p − i + ∑ i [ c t i = x ] [ c t p − i > x ] c t i \sum_x \sum_{i} [\mathrm{ct}_i = x][\mathrm{ct}_{p - i} \le x] \mathrm{ct}_{p - i} + \sum_i [\mathrm{ct}_i = x][\mathrm{ct}_{p - i} > x] \mathrm{ct}_i
x ∑ i ∑ [ c t i = x ] [ c t p − i ≤ x ] c t p − i + i ∑ [ c t i = x ] [ c t p − i > x ] c t i
后两部分都是卷积的形式,使用 FFT 加速计算即可.
这样做的复杂度是 O ( n m log m ) O(\sqrt{n} m \log m) O ( n m log m )
注意到我们还有个简单 O ( n 2 ) O(n^2) O ( n 2 ) B B B c t \mathrm{ct} c t ≤ B \le B ≤ B O ( ( n / B ) 2 ) O((n / B)^2) O ( ( n / B ) 2 ) c t \mathrm{ct} c t > B > B > B O ( B m log m ) O(B m \log m) O ( B m log m ) n , m n, m n , m B = O ( ( n / log n ) 1 / 3 ) B = O\left((n / \log n)^{1 / 3}\right) B = O ( ( n / log n ) 1 / 3 ) O ( n 4 / 3 log 2 / 3 n ) O(n^{4 / 3} \log^{2 / 3} n) O ( n 4 / 3 log 2 / 3 n )
考虑分治,计算跨越分治区间中点的区间贡献.
设分治区间为 [ l , r ] [l, r] [ l , r ] m i d \mathrm{mid} m i d i ∈ [ l , m i d ] i \in [l, \mathrm{mid}] i ∈ [ l , m i d ] j ∈ ( m i d , r ] j \in (\mathrm{mid}, r] j ∈ ( m i d , r ] [ i , j ] [i, j] [ i , j ] [ i , m i d ] [i, \mathrm{mid}] [ i , m i d ] ( m i d , j ] (\mathrm{mid}, j] ( m i d , j ] m i d \mathrm{mid} m i d
通过画画画画画画可以发现,对于一个 i i i ( m i d , r ] (\mathrm{mid}, r] ( m i d , r ] j ∈ ( m i d , x ] j \in (\mathrm{mid}, x] j ∈ ( m i d , x ] [ i , j ] [i, j] [ i , j ] [ i , m i d ] [i, \mathrm{mid}] [ i , m i d ] ( x , y ] (x, y] ( x , y ] [ i , j ] [i, j] [ i , j ] m i d \mathrm{mid} m i d j ∈ ( y , r ] j \in (y, r] j ∈ ( y , r ] [ i , j ] [i, j] [ i , j ] ( m i d , j ] (\mathrm{mid}, j] ( m i d , j ] i i i x x x y y y m i d \mathrm{mid} m i d
问题在于拼接两个区间的直径.注意到如果我们计算出点集的“半径”和“圆心”,点集并的直径长度等于两点集的半径和加上圆心间的距离.半径和容易维护,圆心间的距离造成的贡献形如某个点到区间所有点的距离和,使用 经典技巧 即可快速计算.
带卡时的暴力过了./qd
设 f i , j f_{i, j} f i , j i i i l i l_i l i j j j k k k
{ f k , j + 1 ← f i , j + c l k − s k l k = l i f k , t + 1 ← f i , j + c l k − s k + t o t l k > l i \begin{cases}
f_{k, j + 1} \leftarrow f_{i, j} + c_{l_k} - s_k & l_k = l_i \\
f_{k, t + 1} \leftarrow f_{i, j} + c_{l_k} - s_k + \mathrm{tot} & l_k > l_i
\end{cases}
{ f k , j + 1 ← f i , j + c l k − s k f k , t + 1 ← f i , j + c l k − s k + t o t l k = l i l k > l i
其中 t t t j j j l i l_i l i l k l_k l k t o t \mathrm{tot} t o t 2 2 2 j j j t t t log j \log j log j t = 0 t = 0 t = 0 k < i , l k ≥ l i k < i, l_k \ge l_i k < i , l k ≥ l i
先把每个环边上的颜色薅出来.由于每个环上至少要删一条边,故问题可以被写成一个匹配的形式:我们将每种颜色的边保留一条,然后让剩下的边和环上的颜色匹配.若匹配满了,那么存在一种不消耗颜色的删边方式,直接输出颜色数;若有环未被匹配,说明无论如何都要消耗一种颜色.故答案为 c − ( r − m ) c - (r - m) c − ( r − m ) c c c r r r m m m
直接建图跑网络流即可.由于是二分图,故时间复杂度 O ( n n ) O(n \sqrt{n}) O ( n n )
没写完代码. \Huge\color{red}\text{没写完代码.} 没写完代码.
tsukiotome.
考虑对排列中没有两个相邻元素在树上相邻这一条件容斥.问题转化为钦定排列中有 i i i f u , i , 0 / 1 / 2 f_{u, i, 0 / 1 / 2} f u , i , 0 / 1 / 2 u u u i i i u u u ∧ \land ∧
注意链的方向需要计入方案.
我超,原 .
还没补.
我超,原 .
题解 .
只补了不需要 poly 算法的 70 分,即性质 A.
由于 q 1 = 1 q_1 = 1 q 1 = 1 p i ≥ 1 p_i \ge 1 p i ≥ 1 1 1 1
设 f x ( t ) = P ( x ≤ t ) f_x(t) = P(x \le t) f x ( t ) = P ( x ≤ t ) x ≤ t x \le t x ≤ t x x x 1 − ∫ 0 1 f a 1 ( x ) d x 1 - \int_0^1 f_{a_1}(x) \mathrm{d}x 1 − ∫ 0 1 f a 1 ( x ) d x
先考虑 max \max max f f f s = max { p , q } s = \max\{p, q\} s = max { p , q } f s ( x ) = P ( s ≤ x ) = P ( max { p , q } ≤ x ) = P ( p ≤ x ) P ( q ≤ x ) = f p ( x ) f q ( x ) f_s(x) = P(s \le x) = P(\max\{p, q\} \le x) = P(p \le x) P(q \le x) = f_p(x)f_q(x) f s ( x ) = P ( s ≤ x ) = P ( max { p , q } ≤ x ) = P ( p ≤ x ) P ( q ≤ x ) = f p ( x ) f q ( x )
再考虑 + + + f f f s = p + q s = p + q s = p + q q q q [ 0 , r ] [0, r] [ 0 , r ]
f s ( x ) = P ( p + q ≤ x ) = 1 r ∫ 0 r P ( p + t ≤ x ) d t = 1 r ∫ 0 r f p ( x − t ) d t f_s(x) = P(p + q \le x) = \frac{1}{r} \int_0^r P(p + t \le x) \mathrm{d}t = \frac{1}{r} \int_0^r f_p(x - t) \mathrm{d}t
f s ( x ) = P ( p + q ≤ x ) = r 1 ∫ 0 r P ( p + t ≤ x ) d t = r 1 ∫ 0 r f p ( x − t ) d t
若令 F p ( x ) F_p(x) F p ( x ) f p ( x ) f_p(x) f p ( x ) f s ( x ) = 1 r ( F ( x − 0 ) − F ( x − r ) ) f_s(x) = \frac{1}{r} (F(x - 0) - F(x - r)) f s ( x ) = r 1 ( F ( x − 0 ) − F ( x − r ) ) q 1 = 1 q_1 = 1 q 1 = 1 f a 1 ( x ) f_{a_1}(x) f a 1 ( x ) [ 0 , 1 ] [0, 1] [ 0 , 1 ] + + + f s ( x ) = 1 r F p ( x ) f_s(x) = \frac{1}{r} F_p(x) f s ( x ) = r 1 F p ( x )
再考虑乘 k k k f f f s = k p s = kp s = k p f s ( x ) = f p ( x / k ) f_s(x) = f_p(x / k) f s ( x ) = f p ( x / k )
再考虑乘方操作对 f f f s = p k s = p^k s = p k f s ( x ) = f p ( x 1 / k ) f_s(x) = f_p\left(x^{1 / k}\right) f s ( x ) = f p ( x 1 / k )
由于叶子上的 f f f 1 1 1 f f f
注意到乘 k k k 998244353 998244353 9 9 8 2 4 4 3 5 3
保序回归,先套个板子,问题转化为将 x x x x + ϵ x + \epsilon x + ϵ
什么 b 东西.
我超,原 .
先建出等价流树,问题转化为:你需要给出一个首尾相接的排列,价值定义为 p i p_i p i p i + 1 p_{i + 1} p i + 1
经过猜猜猜得出,所有树边都可以被取到,然后权值最小的边会被取到 2 2 2
权值最小的边会被取到 2 2 2 S S S T T T i i i p i ∈ S p_i \in S p i ∈ S p i + 1 ∈ T p_{i + 1} \in T p i + 1 ∈ T j ≠ i j \not= i j = i p j ∈ T , p j + 1 ∈ S p_j \in T, p_{j + 1} \in S p j ∈ T , p j + 1 ∈ S
上述过程给我们了一个关于构造方案的启示:我们可以每次删除当前连通块内权值最小的边,这样就变成了两个子问题,递归做即可.
什么 b 东西.
唐.直接上 AC 自动机就做完了.
考虑将贡献拆到边上,计算一条边 ( u , v , w ) (u, v, w) ( u , v , w ) w w w
考虑求最大权生成基环森林的过程,我们可以将边按边权降序排序,贪心选取.边 ( u , v , w ) (u, v, w) ( u , v , w ) 2 2 2
u u u v v v u u u v v v u u u S S S v v v T T T S S S T T T
那么 ( u , v , w ) (u, v, w) ( u , v , w )
联通块是基环树这一条件并不方便刻画,考虑计算反面,即 ( u , v , w ) (u, v, w) ( u , v , w )
u u u v v v u u u v v v
条件里只剩联通和树了,又我们只关心权值比 w w w f S f_S f S S S S g S g_S g S S S S S S S c S c_S c S S S S T T T
f S = 1 ∣ S ∣ − 1 ∑ T f T f S − T ( c S − ( c T + c S − T ) ) g S = 2 c S − ∑ T 2 c S − T g T \begin{aligned}
f_S &= \frac{1}{|S| - 1} \sum_T f_T f_{S - T} (c_S - (c_T + c_{S - T})) \\
g_S &= 2^{c_S} - \sum_T 2^{c_{S - T}} g_T \\
\end{aligned}
f S g S = ∣ S ∣ − 1 1 T ∑ f T f S − T ( c S − ( c T + c S − T ) ) = 2 c S − T ∑ 2 c S − T g T
f f f 1 ∣ S ∣ − 1 \frac{1}{|S| - 1} ∣ S ∣ − 1 1 ∣ S ∣ − 1 |S| - 1 ∣ S ∣ − 1
于是我们可以在 O ( 3 n ) O(3^n) O ( 3 n ) f f f g g g U U U ( u , v , w ) (u, v, w) ( u , v , w )
1 2 ( 1 − 1 2 c U ( ∑ u , v ∈ S 2 c U − S ( g S − f S ) + ∑ u ∈ S v ∉ S ∑ T ⊆ U − S v ∈ T 2 c U − S − T ( g S − f S ) ( g T − f T ) ) ) \frac{1}{2} \left(1 - \frac{1}{2^{c_U}} \left(\sum_{u, v \in S} 2^{c_{U - S}} (g_S - f_S) + \sum_{\substack{u \in S \\ v \not\in S}} \sum_{\substack{T \subseteq U - S \\ v \in T}} 2^{c_{U - S - T}} (g_S - f_S) (g_T - f_T)\right)\right)
2 1 ⎝ ⎜ ⎜ ⎛ 1 − 2 c U 1 ⎝ ⎜ ⎜ ⎛ u , v ∈ S ∑ 2 c U − S ( g S − f S ) + u ∈ S v ∈ S ∑ T ⊆ U − S v ∈ T ∑ 2 c U − S − T ( g S − f S ) ( g T − f T ) ⎠ ⎟ ⎟ ⎞ ⎠ ⎟ ⎟ ⎞
口胡了一下,不知道对不对.
首先我们有无根树哈希,可以快速判断两个无标号无根树是否相同,做法就是选重心为根哈希,若有两个重心就都哈希一遍,然后随便你保留小的或者异或到一起.
设第一遍删完后的图为 S S S T T T S S S B B B T T T A A A B B B
首先先进行一个 Min-Max 容斥,设随机变量 x i x_i x i i i i E ( max x i ) E(\max x_i) E ( max x i )
E ( max x i ) = ∑ S ( − 1 ) ∣ S ∣ + 1 E ( min i ∈ S x i ) E(\max x_i) = \sum_S (-1)^{|S| + 1} E\left(\min_{i \in S} x_i\right)
E ( max x i ) = S ∑ ( − 1 ) ∣ S ∣ + 1 E ( i ∈ S min x i )
考虑如何对所有子集 S S S E ( min i ∈ S x i ) E(\min_{i \in S} x_i) E ( min i ∈ S x i ) S S S p S p_S p S E ( min i ∈ S x i ) = 1 + p S / ( 1 − p S ) E(\min_{i \in S} x_i) = 1 + p_S / (1 - p_S) E ( min i ∈ S x i ) = 1 + p S / ( 1 − p S )
考虑如何计算取得长度为 m m m r 1 , r 2 , ⋯ , r m r_1, r_2, \cdots, r_m r 1 , r 2 , ⋯ , r m r 1 r_1 r 1 1 / n 1 / n 1 / n i > 1 i > 1 i > 1 r i r_i r i 1 / ( n − r i − 1 ) 1 / (n - r_{i - 1}) 1 / ( n − r i − 1 ) r m = n r_m = n r m = n
p S = 1 n ∏ i ∈ U − S i ≠ n 1 n − i p_S = \frac{1}{n} \prod_{\substack{i \in U - S \\ i \not= n}} \frac{1}{n - i}
p S = n 1 i ∈ U − S i = n ∏ n − i 1
然后就直接按照容斥式子计算即可.
先考虑如何做 0 ≤ s ≤ t 0 \le s \le t 0 ≤ s ≤ t t t t ≥ t \ge t ≥ t
∑ i ≥ t ( n i ) \sum_{i \ge t} \binom{n}{i}
i ≥ t ∑ ( i n )
现在考虑计算越过 t t t t t t p p p t t t 2 t − p 2t - p 2 t − p 2 t − p 2t - p 2 t − p
∑ i < t ( n 2 t − i ) \sum_{i < t} \binom{n}{2t - i}
i < t ∑ ( 2 t − i n )
预处理组合数前缀和即可计算.
对于 s > t s > t s > t s s s t t t
什么 b 东西.
设 f x f_x f x ≥ x \ge x ≥ x ∑ f i \sum f_i ∑ f i
考虑如何计算 f x f_x f x v a l \mathrm{val} v a l ≥ x \ge x ≥ x 1 1 1 < x < x < x 0 0 0 01 01 0 1 1 1 1 S S S g S g_S g S
∑ i = 1 m ∑ S g S ( m − i + 1 ) ∣ S ∣ ( i − 1 ) n − ∣ S ∣ = ∑ S g S ∑ i = 1 m ( m − i + 1 ) ∣ S ∣ ( i − 1 ) n − ∣ S ∣ \sum_{i = 1}^m \sum_S g_S (m - i + 1)^{|S|} (i - 1)^{n - |S|} = \sum_S g_S \sum_{i = 1}^m (m - i + 1)^{|S|} (i - 1)^{n - |S|}
i = 1 ∑ m S ∑ g S ( m − i + 1 ) ∣ S ∣ ( i − 1 ) n − ∣ S ∣ = S ∑ g S i = 1 ∑ m ( m − i + 1 ) ∣ S ∣ ( i − 1 ) n − ∣ S ∣
后面那个 ∑ \sum ∑ O ( n 2 ) O(n^2) O ( n 2 )
但是枚举大小为 n n n ∣ S ∣ |S| ∣ S ∣ ∣ S ∣ = i |S| = i ∣ S ∣ = i 1 1 1
对 n n n
n = 1 n = 1 n = 1
此时你无法区分每道题目,故此时直接讨论是否和给定的人反选即可.
n = 2 n = 2 n = 2
此时第二个人和第一个人选择不同的题目和选择相同的题目可以被区分,故设 c 0 , c 1 c_0, c_1 c 0 , c 1 x 0 , x 1 x_0, x_1 x 0 , x 1
x 0 + x 1 = s 1 c 0 − x 0 + x 1 = s 2 \begin{aligned}
x_0 + x_1 &= s_1 \\
c_0 - x_0 + x_1 &= s_2
\end{aligned}
x 0 + x 1 c 0 − x 0 + x 1 = s 1 = s 2
容易解出 x 0 , x 1 x_0, x_1 x 0 , x 1 x x x y y y max { x , y } x + y \frac{\max\{x, y\}}{x + y} x + y m a x { x , y }
n = 3 n = 3 n = 3
和 n = 2 n = 2 n = 2 4 4 4 3 3 3
对于更一般的情况,采取这个做法会导致需要解一个 2 n − 1 2^{n - 1} 2 n − 1 n n n
我草这 jb 啥啊?
首先不知道为什么题目中给出的图是平面三角剖分图,然后由四色定理可知,色数 ≤ 4 \le 4 ≤ 4
我们只需对色数等于 1 , 2 , 3 1, 2, 3 1 , 2 , 3 1 1 1
然后我们发现,随着区间增长,色数单调不降.故我们可以计算出 m x 2 r i \mathrm{mx2r}_i m x 2 r i j j j [ i , j ] [i, j] [ i , j ] 2 2 2 m x 3 r i \mathrm{mx3r}_i m x 3 r i j j j [ i , j ] [i, j] [ i , j ] 3 3 3
m x 2 r i \mathrm{mx2r}_i m x 2 r i i i i m x 3 r i \mathrm{mx3r}_i m x 3 r i
一个平面三角剖分图是可以被 3-染色的,当且仅当它的面可被 2-染色.
而这个条件又等价于,平面嵌入中不与外部面相接的顶点度数均为偶数.不与外部面相接的顶点即为前后第一个大于 / 小于它的点都已经和它连边的点,容易双指针维护.
上述引理证明的讨论可见这个链接:Link .
首先,由于 1 1 1 c 1 , c 2 c_1, c_2 c 1 , c 2 1 1 1 x x x x + ( k − x − ( c 1 − x ) − ( c 2 − x ) ) = k − c 1 − c 2 + 2 x x + (k - x - (c_1 - x) - (c_2 - x)) = k - c_1 - c_2 + 2x x + ( k − x − ( c 1 − x ) − ( c 2 − x ) ) = k − c 1 − c 2 + 2 x x x x
将每个操作看成一个置换,序列 a a a [ l , r ] [l, r] [ l , r ] b b b a a a [ l , r ] [l, r] [ l , r ] b b b a a a [ l , n ] [l, n] [ l , n ] b b b [ r + 1 , n ] [r + 1, n] [ r + 1 , n ]
设 f S f_S f S a a a S S S g S g_S g S b b b S S S ≥ m \ge m ≥ m
考虑如何对某一个 x x x = x = x = x
考虑只由 < x < x < x > x > x > x v v v [ v > x ] [v > x] [ v > x ] f i f_i f i 0 / 1 0 / 1 0 / 1 f i ≠ f i + 1 f_i \not= f_{i + 1} f i = f i + 1 g i = [ f i ≠ f i + 1 ] g_i = [f_i \not= f_{i + 1}] g i = [ f i = f i + 1 ] g g g 1 1 1
事实上 g g g 1 1 1 l l l ⌈ l / 2 ⌉ \lceil l / 2 \rceil ⌈ l / 2 ⌉ f f f 0 / 1 0 / 1 0 / 1 0 0 0 1 1 1 0 / 1 0 / 1 0 / 1
然后发现这玩意可以上线段树就做完了.
注意到 h e i g h t \mathrm{height} h e i g h t
考虑在原串上限制 i i i j j j s a i \mathrm{sa}_i s a i r k i \mathrm{rk}_i r k i r k i \mathrm{rk}_i r k i r k j \mathrm{rk}_j r k j
再考虑构造字典序最小的串,对于某个 i i i h e i g h t i = − 1 \mathrm{height}_i = -1 h e i g h t i = − 1 r k s a i + 1 ≤ r k s a i − 1 + 1 \mathrm{rk}_{\mathrm{sa}_i + 1} \le \mathrm{rk}_{\mathrm{sa}_{i - 1} + 1} r k s a i + 1 ≤ r k s a i − 1 + 1 s a i \mathrm{sa}_i s a i i i i s s a i > s s a i − 1 s_{\mathrm{sa}_i} > s_{\mathrm{sa}_{i - 1}} s s a i > s s a i − 1
我超,原 .
显然边双内的边都能无条件断开,其他的边断了一定不优秀(会舍弃边双树子树中的点),故答案就是只走割边的联通块个数.
首先题意转化后就是要你做异或 ( min , + ) (\min, +) ( min , + )
我们有非常好数据随机保证,故打个表先.发现数组中不同的值很少!!!111
发现一个方案若能凑出来 x x x ≤ x \le x ≤ x min \min min
压力给到如何快速求得 x x x ≤ y \le y ≤ y x and y x \operatorname{and} y x a n d y 1 1 1 1 1 1 or \operatorname{or} o r