100 + 30 + 0 + 100.
二维 ST 表弄个关于颜色的 bitset,然后就可以二分了.
诈骗题.一眼看到了一个不弱于快速阶乘算法的东西,然而模数够小,于是 n n n
d = 1 d = 1 d = 1 d d d
即对 npc 创不死玩家的地图计数.注意到由于玩家左侧只会有 slime,且人类只能通过 slime 来刷级,所以 npc 能够创死在 i i i > s i + i − 1 > s_i + i - 1 > s i + i − 1
直接钦定 i i i n n n
注意到任何时刻序列单调不升,所以考虑维护轮廓线.
用 set 维护拐点即可.细节有点多.
当然也可以线段树!只是我傻逼了没想到.
100 + 50 + 50 + 100.
考虑算出 n ! n! n ! a i ≤ 2 × 1 0 5 a_i \le 2 \times 10^5 a i ≤ 2 × 1 0 5 2 × 1 0 5 2 \times 10^5 2 × 1 0 5
然后给 a a a
典中典区间 DP,为啥写挂了呢.
设 f l , r f_{l, r} f l , r [ l , r ] [l, r] [ l , r ] k − 1 k - 1 k − 1
首先注意到对于互相包含的限制区间,大的那个没用,直接去掉.问题转化为对多个互不包含的区间限制计算方案数.
这个限制不漂亮,考虑计算对于所有的区间,内部都不存在相同数的序列数量.
把区间按照右端点升序排序,考虑设计一个 DP.设 f i , j f_{i, j} f i , j i i i j j j
若相交,发现相交部分已经处理过,只需处理新增部分的方案数.
若不相交,需乘上中间部分随便选的方案数.
然而这样时间复杂度是 O ( n 3 ) O(n^3) O ( n 3 ) j j j 0 / 1 0 / 1 0 / 1
首先先二分,转化成对 < λ < \lambda < λ
记录一个全集的值域线段树,再对每个点记录其邻接边的值域线段树.若查询的 k k k
若 k k k 1 1 1
50 + 100 + 70 + 0.
乱搞一下就 50 分,再乱搞一下就过了.
不是很懂啊.
不难发现和自己子树中最浅的没有匹配过的点匹配是最优的.线段树合并即可.
考虑优化建图,对每一位建一个虚点,若 a i a_i a i j j j 1 1 1 i i i j j j a i a_i a i
然而这样需要跑 n n n u → u \to u → → ⋯ → \to \cdots \to → ⋯ → → v \to v → v u u u v v v O ( n log 2 n ) O(n \log^2 n) O ( n log 2 n )
预处理虚点 → v \to v → v O ( n log n ) O(n \log n) O ( n log n )
巨大恶心 DP.
注意到每次划分出的集合是确定的,故可以设 f i , S , j f_{i, S, j} f i , S , j S S S i i i j j j
转移枚举分割出的两部分 P P P Q Q Q x x x y y y
f i , S , j = min x , y f i , P , x + dist ( x , y ) + f y , Q , j f_{i, S, j} = \min_{x, y} f_{i, P, x} + \operatorname{dist}(x, y) + f_{y, Q, j}
f i , S , j = x , y min f i , P , x + d i s t ( x , y ) + f y , Q , j
根据经典结论,这个状态数是 O ( n 2 ) O(n^2) O ( n 2 )
然后预处理所有 x x x min y dist ( x , y ) + f y , Q , j \min\limits_y \operatorname{dist}(x, y) + f_{y, Q, j} y min d i s t ( x , y ) + f y , Q , j O ( n 3 ) O(n^3) O ( n 3 )
100 + 0 + 100 + 0.
对质因子根号分治,小于 1 0 9 \sqrt{10^9} 1 0 9 1 0 9 \sqrt{10^9} 1 0 9 n n n
大搜索.不会.
设 d i d_i d i [ 1 , i ] [1, i] [ 1 , i ] [ l , r ] [l, r] [ l , r ] d r − d l − 1 1 0 r − l + 1 ≡ 0 ( m o d p ) d_r - d_{l - 1} 10^{r - l + 1} \equiv 0 \pmod p d r − d l − 1 1 0 r − l + 1 ≡ 0 ( m o d p )
整理一下式子,即对 l ≤ x < y ≤ r l \le x < y \le r l ≤ x < y ≤ r d x 1 0 y − x ≡ d y ( m o d p ) d_x 10^{y - x} \equiv d_y \pmod p d x 1 0 y − x ≡ d y ( m o d p )
考虑分治.设当前分治区间为 [ l , r ] [l, r] [ l , r ] m = ⌊ ( l + r ) / 2 ⌋ m = \lfloor (l + r) / 2 \rfloor m = ⌊ ( l + r ) / 2 ⌋ ( x , y ) (x, y) ( x , y ) d x 1 0 m − x 1 0 y − m ≡ d y ( m o d p ) d_x 10^{m - x} 10^{y - m} \equiv d_y \pmod p d x 1 0 m − x 1 0 y − m ≡ d y ( m o d p ) f i f_i f i [ l , m ] [l, m] [ l , m ] d x 1 0 m − x = i d_x 10^{m - x} = i d x 1 0 m − x = i x x x g i , j g_{i, j} g i , j [ m + 1 , r ] [m + 1, r] [ m + 1 , r ] 1 0 y − m = i 10^{y - m} = i 1 0 y − m = i f y = j f_y = j f y = j y y y i = d x 1 0 m − x i = d_x 10^{m - x} i = d x 1 0 m − x j = 1 0 y − m j = 10^{y - m} j = 1 0 y − m ∑ i ∑ j f i × g j , i j \sum_i \sum_j f_i \times g_{j, ij} ∑ i ∑ j f i × g j , i j
此时不带修的问题已经可以通过离线询问后一遍分治解决,考虑带修,发现分治过程中维护的信息数量是 Θ ( p 2 ) \Theta(p^2) Θ ( p 2 )
时间复杂度 Θ ( n p 2 log n ) \Theta(n p^2 \log n) Θ ( n p 2 log n )
大 DP,不会.
100 + 100 + 10 + 0.
并查集搞搞就做完了.
显然对于形态相同的树,方案数是一样的.
考虑设 f S f_S f S S S S S S S m m m
考虑计算所有形态为 S ′ S^\prime S ′ c t \mathrm{ct} c t c t \mathrm{ct} c t f S ′ f_{S^\prime} f S ′ ( c t + f S ′ − 1 f S ′ − 1 ) \binom{\mathrm{ct} + f_{S^\prime} - 1}{f_{S^\prime} - 1} ( f S ′ − 1 c t + f S ′ − 1 )
那么对于形态为 S S S S ′ S^\prime S ′ ct ( S ′ ) \operatorname{ct}(S^\prime) c t ( S ′ )
f S = m ∏ S ′ ( ct ( S ′ ) + f S ′ − 1 f S ′ − 1 ) f_S = m \prod_{S^\prime} \binom{\operatorname{ct}(S^\prime) + f_{S^\prime} - 1}{f_{S^\prime} - 1}
f S = m S ′ ∏ ( f S ′ − 1 c t ( S ′ ) + f S ′ − 1 )
注意到这个组合数不能直接算,但是其等于 ( c t + f S ′ − 1 c t ) \binom{\mathrm{ct} + f_{S^\prime} - 1}{\mathrm{ct}} ( c t c t + f S ′ − 1 ) ∑ c t = O ( n ) \sum \mathrm{ct} = O(n) ∑ c t = O ( n )
如何记录形态到状态里?树哈希或者 std::map<std::multiset<int>, int> 映射.
A334551 .
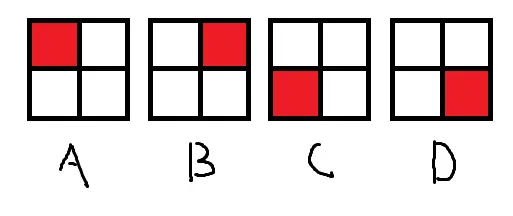
容易发现一个 2 × 2 2 \times 2 2 × 2 n × n n \times n n × n 4 4 4 4 4 4
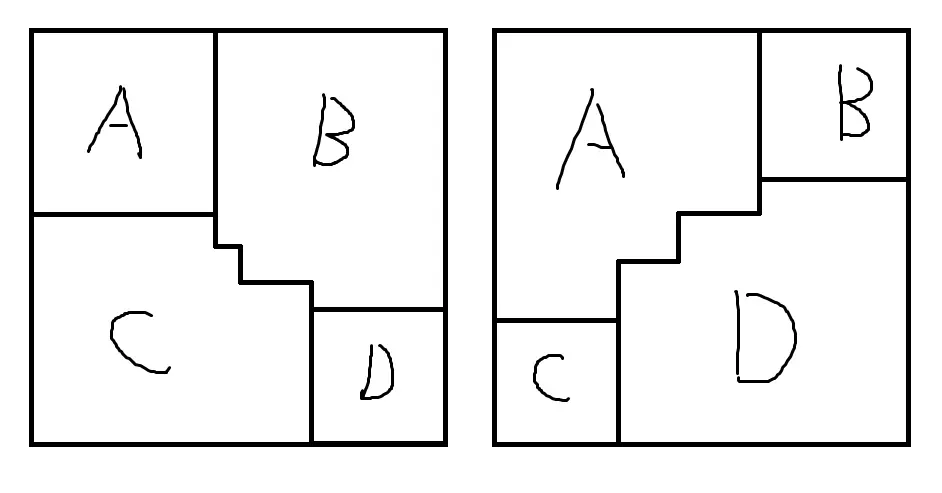
对于横着的两个格子,若右边的确定为 A,则左边的也要是 A,但确定左边时右边有多种可能.BCD 的情况类似.于是我们可以得到,最终的填入方案一定形如下图:
那么枚举折线的起止点,方案数为:
∑ 0 < a < n ∑ 0 < b < n ∑ a ≤ c < n ∑ b ≤ d < n ( c − a + d − b c − a ) + 2 ∑ i < n ∑ j < n ( i + j i ) + ( 2 n n ) \sum_{0 < a < n} \sum_{0 < b < n} \sum_{a \le c < n} \sum_{b \le d < n} \binom{c - a + d - b}{c - a} + 2\sum_{i < n} \sum_{j < n} \binom{i + j}{i} + \binom{2n}{n}
0 < a < n ∑ 0 < b < n ∑ a ≤ c < n ∑ b ≤ d < n ∑ ( c − a c − a + d − b ) + 2 i < n ∑ j < n ∑ ( i i + j ) + ( n 2 n )
又由于矩阵可以旋转 90 90 9 0 s s s 2 s − ( n + 1 ) 2 2s - (n + 1)^2 2 s − ( n + 1 ) 2
稍微推推就能得到答案为
8 ( 2 n n ) − 3 ( n + 1 ) 2 + 4 ( n + 1 ) − 8 8\binom{2n}{n} - 3(n + 1)^2 + 4(n + 1) - 8
8 ( n 2 n ) − 3 ( n + 1 ) 2 + 4 ( n + 1 ) − 8
大构造.不会.
100 + 100 + 0 + 0.
发现题目中的那个诡异操作就是将 a i , a j , a k a_i, a_j, a_k a i , a j , a k 2 2 2 10 10 1 0 j j j a j a_j a j P P P a i a_i a i a k a_k a k
发现撤销某个操作会导致一段后缀的点发生平移,于是枚举删的是哪个操作,倒着扣一遍贡献,过程中记录答案即可.
神仙.
如果我们确定了第 i i i c i c_i c i
( n c 1 , c 2 , ⋯ , c k ) = ( n c 1 ) ( n − c 1 c 2 ) ( n − c 1 − c 2 c 3 ) ⋯ ( n − c 1 − c 2 − ⋯ − c k − 1 c k ) \binom{n}{c_1, c_2, \cdots, c_k} = \binom{n}{c_1} \binom{n - c_1}{c_2} \binom{n - c_1 - c_2}{c_3} \cdots \binom{n - c_1 - c_2 - \cdots - c_{k - 1}}{c_k}
( c 1 , c 2 , ⋯ , c k n ) = ( c 1 n ) ( c 2 n − c 1 ) ( c 3 n − c 1 − c 2 ) ⋯ ( c k n − c 1 − c 2 − ⋯ − c k − 1 )
考虑这个东西 m o d 2 \bmod\ 2 m o d 2 ≠ 0 \not= 0 = 0 ≠ 0 \not= 0 = 0
回忆 Lucas 定理,( n m ) m o d 2 ≠ 0 \binom{n}{m} \bmod 2 \not= 0 ( m n ) m o d 2 = 0 s ( n ) s(n) s ( n ) n n n 1 1 1 s ( m ) ⊆ s ( n ) s(m) \subseteq s(n) s ( m ) ⊆ s ( n )
若上式 ≠ 0 \not= 0 = 0 ( n c 1 ) \binom{n}{c_1} ( c 1 n ) s ( c 1 ) ⊆ s ( n ) s(c_1) \subseteq s(n) s ( c 1 ) ⊆ s ( n ) n − c 1 n - c_1 n − c 1 ( n − c 1 c 2 ) \binom{n - c_1}{c_2} ( c 2 n − c 1 ) s ( c 2 ) ⊆ s ( n − c 1 ) s(c_2) \subseteq s(n - c_1) s ( c 2 ) ⊆ s ( n − c 1 ) n − c 1 − c 2 n - c_1 - c_2 n − c 1 − c 2
⋃ i = 1 k s ( c i ) = s ( n ) \bigcup\limits_{i = 1}^k s(c_i) = s(n) i = 1 ⋃ k s ( c i ) = s ( n ) ∀ i ≠ j , s ( c i ) ∩ s ( c j ) = ∅ \forall i \not= j, s(c_i) \cap s(c_j) = \varnothing ∀ i = j , s ( c i ) ∩ s ( c j ) = ∅
即对于所有 i i i s ( c i ) s(c_i) s ( c i ) s ( n ) s(n) s ( n )
那么我们可以从低到高考虑对于 n n n 1 1 1 c i c_i c i S S S m m m S S S O ( a k ) O(a_k) O ( a k ) std::bitset 记录,时间复杂度 O ( k V log n / w ) O(kV \log n / w) O ( k V log n / w ) V = max a i V = \max a_i V = max a i w w w
太厉害了,不会做.
考虑这个东西的含义,发现就是最大化有 n n n k k k
可以考虑一个简单的构造,就是将 n n n k k k T n , k T_{n, k} T n , k T n , k T_{n, k} T n , k n n n k k k 1 1 1 Turán 定理 ,这个图的边数是
( n − m 2 ) + ( k − 1 ) ( m + 1 2 ) \binom{n - m}{2} + (k - 1)\binom{m + 1}{2}
( 2 n − m ) + ( k − 1 ) ( 2 m + 1 )
其中 m = ⌊ n / k ⌋ m = \lfloor n / k \rfloor m = ⌊ n / k ⌋
为啥这么构造就能达到上界呢,不懂.
换根倍增.
分层图最短路即可.层和层之间可以使用 DP 转移,但貌似直接转移也不会寄?
没写代码.
\Huge \red{\text{没写代码.}}
没写代码.
首先计算 f n f_n f n f f f
考虑计算 gcd ( a 1 f n + a 2 f n + 1 , b 1 f n + b 2 f n + 1 ) \gcd(a_1 f_n + a_2 f_{n + 1}, b_1 f_n + b_2 f_{n + 1}) g cd( a 1 f n + a 2 f n + 1 , b 1 f n + b 2 f n + 1 ) b 2 b_2 b 2 gcd ( a 1 ′ f n + a 2 ′ f n + 1 , b 1 ′ f n ) \gcd({a_1}^\prime f_n + {a_2}^\prime f_{n + 1}, {b_1}^\prime f_n) g cd( a 1 ′ f n + a 2 ′ f n + 1 , b 1 ′ f n )
但是目前计算两边的真实值仍然是不可接受的,考虑继续减小值的规模.若我们计算出了 g = gcd ( a 1 ′ f n + a 2 ′ f n + 1 , f n ) = gcd ( a 2 ′ , f n ) ≤ 400 g = \gcd({a_1}^\prime f_n + {a_2}^\prime f_{n + 1}, f_n) = \gcd({a_2}^\prime, f_n) \le 400 g = g cd( a 1 ′ f n + a 2 ′ f n + 1 , f n ) = g cd( a 2 ′ , f n ) ≤ 4 0 0 gcd ( a 1 ′ f n + a 2 ′ f n + 1 , b 1 ′ f n ) = gcd ( a 1 ′ f n + a 2 ′ f n + 1 , b 1 ′ g ) \gcd({a_1}^\prime f_n + {a_2}^\prime f_{n + 1}, {b_1}^\prime f_n) = \gcd({a_1}^\prime f_n + {a_2}^\prime f_{n + 1}, {b_1}^\prime g) g cd( a 1 ′ f n + a 2 ′ f n + 1 , b 1 ′ f n ) = g cd( a 1 ′ f n + a 2 ′ f n + 1 , b 1 ′ g )