显然只会去换两国货币面值最小的那一种货币,直接枚举某国的换多少即可.
一眼的贪心假了./ll
第一问直接选择当前能到的点中编号最小的那一个即可.
第二问不能贪心选最大的访问,因为当前可以访问的节点中可能有些可以访问且不会造成代价的节点,先访问这些节点可能可以解锁一些编号更大的点.于是先将可以走完的点走完再取最大的即可.
原题是 gym101821B .
注意到选出的 LIS 和 LDS 中一定存在一个位置,使得在这一位置之前,LDS 的所有元素大于 LIS 的所有元素,在这位置之后,LDS 的所有元素都小于 LIS 的元素.我们称这一位置为“交点”.
考虑枚举 LIS 中交点前的一个位置 i i i i i i i i i
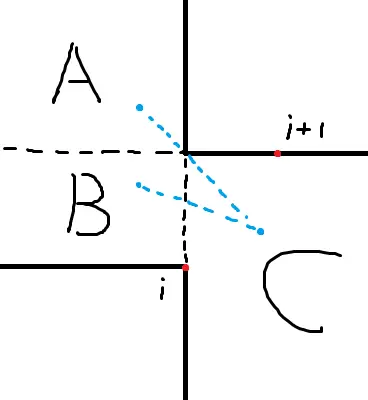
考虑可以选择哪些位置的两个点拼接起来.如下图:
其中红点是在 LIS 中相邻的两个元素,我们需要在 A 或 B 区间中选择某个元素,然后再从 C 中选择一个元素,使得以第一个选择的元素结尾的 LDS 拼上以第二个选择的元素为开头的 LDS 长度等于全局 LDS.若能选出来,显然能给出一组合法构造.
如何选?先考虑 A,C 两区域内选元素的方案,这显然在两部分中贪心选最长的即可,因为有 i + 1 i + 1 i + 1
B,C 区域选元素的方案貌似不好统计,但是我们可以维护一个处于 LDS 中的元素,他可选的后继元素最远在哪.若 B 区域中的元素后继最远距离超过 i i i
代码非常 /tuu.
显然由于权值互不相同,好路径的条数不超过 n n n
考虑一个过程,从 0 0 0 L L L = L = L = L x x x 1 1 1 x x x
先考虑路径祖先到儿子的情况,我们只需维护加入权值 ≤ i \le i ≤ i 1 1 1 O ( 1 ) O(1) O ( 1 ) 1 1 1
再考虑路径是 u u u w w w w w w v v v w w w u u u v v v w w w L L L std::set 维护,我们只需要找到这个区间内合法的位置有多少个,即对等于 2 2 2 2 2 2
首先每位独立,然后只需计算出有几位可以填两种值,分讨即可.
首先可以通过一些交换,将所有情况转化为 x u < x v x_u < x_v x u < x v y u < y v y_u < y_v y u < y v
由于查询矩形被 u u u v v v
x − x u + y − y u < x v − x + y v − y ⟺ y < − x + x u + y u + x v + y v 2 x - x_u + y - y_u < x_v - x + y_v - y \iff y < -x + \frac{x_u + y_u + x_v + y_v}{2}
x − x u + y − y u < x v − x + y v − y ⟺ y < − x + 2 x u + y u + x v + y v
发现答案形如矩形内在某条直线下方的整点数.事实上我们只需算出 x x x − 1 -1 − 1 0 0 0
拜谢 ckain.
不妨令全局权值和为 s s s u u u s u m u \mathrm{sum}_u s u m u
先考虑没有选择点集限制的时候怎么做.由于选择 u u u max { max v s u m v , s − s u m u } \max\{\max_v \mathrm{sum}_v, s - \mathrm{sum}_u\} max { max v s u m v , s − s u m u } max \max max s u m u ≥ s 2 \mathrm{sum}_u \ge \frac{s}{2} s u m u ≥ 2 s
现在考虑如何查询,对于链上的点,显然选最深的那一个点的最大子树,轻重链剖分后维护区间 s u m u \mathrm{sum}_u s u m u s − s u m u s - \mathrm{sum}_u s − s u m u O ( log n ) O(\log n) O ( log n ) s u m u \mathrm{sum}_u s u m u
考虑带上点集限制怎么做.对于不在链上的点,直接将不能选的位置赋值成 − ∞ -\infty − ∞
时间复杂度 O ( n log 2 n ) O(n \log^2 n) O ( n log 2 n )
太困难!!!
暴力即可.
首先,( gcd , l e n ) (\gcd, \mathrm{len}) ( g cd, l e n ) O ( d ( n ) ) O(d(n)) O ( d ( n ) ) gcd \gcd g cd
有一个 naive 的想法是,我们统计包含 i i i c t i \mathrm{ct}_i c t i ( i , l e n ) (i, \mathrm{len}) ( i , l e n ) ( c t i l e n ) \binom{\mathrm{ct}_{i}}{\mathrm{len}} ( l e n c t i ) gcd \gcd g cdi i i f i f_i f i gcd = i \gcd = i g cd= i
( c t i l e n ) = ∑ i ∣ d f d \binom{\mathrm{ct}_{i}}{\mathrm{len}} = \sum_{i | d} f_d
( l e n c t i ) = i ∣ d ∑ f d
这不是我们 Mobius 反演的题目吗!直接反演得到
f i = ∑ i ∣ d μ ( d / i ) ( c t d l e n ) f_i = \sum_{i | d} \mu(d / i) \binom{\mathrm{ct}_{d}}{\mathrm{len}}
f i = i ∣ d ∑ μ ( d / i ) ( l e n c t d )
然后就可以 O ( n + n log n ) O(\sqrt{n} + n \log n) O ( n + n log n )
由于 i i i O ( V ) O(V) O ( V ) O ( log V ) O(\log V) O ( log V )
此时直接搜索的复杂度是 O ( V ) O(V) O ( V ) O ( V ) O(\sqrt{V}) O ( V )
31 31 3 1 998244352 998244352 9 9 8 2 4 4 3 5 2 31 31 3 1 3 1 − 1 31^{-1} 3 1 − 1
太困难!!!
考虑第一次询问什么.假如第一次询问 i i i ≥ i \ge i ≥ i ≤ k \le k ≤ k f i f_i f i [ 1 , i ] [1, i] [ 1 , i ]
f i = max j ≤ i { f j − 1 − k + j ( i − j + 1 ) } f_i = \max_{j \le i} \{f_{j - 1 - k} + j(i - j + 1)\}
f i = j ≤ i max { f j − 1 − k + j ( i − j + 1 ) }
这个时候已经可以斜率优化了,但是我打表发现决策点单调增,直接双指针就能过去.
先给树随便定个根.
考虑将 u u u 0 ∼ ∣ C u ∣ − 1 0 \sim |C_u| - 1 0 ∼ ∣ C u ∣ − 1 C u C_u C u u u u
这样就只剩下去掉 u u u n − 2 n - 2 n − 2
设 f S , T f_{S, T} f S , T S S S T T T d i s \mathrm{dis} d i s O ( n 4 n ) O(n4^n) O ( n 4 n )
显然跑不动一点,但是我们可以让 T T T S S S d i s \mathrm{dis} d i s d i s \mathrm{dis} d i s O ( n 3 n ) O(n3^n) O ( n 3 n )
太困难!!!
记 c i c_i c i a x ≡ i ( m o d 9 ) a_x \equiv i \pmod 9 a x ≡ i ( m o d 9 ) x x x 3 3 3 i i i
先将有交的路径并起来,这个可以直接暴力实现.
然后问题转化经典的 01 背包,注意到物品的重量和为 n n n O ( n ) O(\sqrt{n}) O ( n )
注意到出题人非常友善,查询区间长度形如 2 k 2^k 2 k
先考虑不带修改怎么做,我们可以预处理 m x k , i \mathrm{mx}_{k, i} m x k , i [ i , i + 2 k ) [i, i + 2^k) [ i , i + 2 k ) s u m k , i \mathrm{sum}_{k, i} s u m k , i [ i , i + 2 k ) [i, i + 2^k) [ i , i + 2 k )
s u m k , i = s u m k − 1 , i + s u m k − 1 , i + 2 k − 1 + m x k , i \mathrm{sum}_{k, i} = \mathrm{sum}_{k - 1, i} + \mathrm{sum}_{k - 1, i + 2^{k - 1}} + \mathrm{mx}_{k, i}
s u m k , i = s u m k − 1 , i + s u m k − 1 , i + 2 k − 1 + m x k , i
现在考虑带上修改,然后我们发现这个类似 ST 表的东西根本修不动.这时我们考虑一个根号分治,设置阈值 B = 2 k B = 2^k B = 2 k i ≤ k i \le k i ≤ k m x i , j \mathrm{mx}_{i, j} m x i , j s u m i , j \mathrm{sum}_{i, j} s u m i , j O ( B ) O(B) O ( B ) > B > B > B O ( n / B + B ) O(n / B + B) O ( n / B + B ) B B B n \sqrt{n} n k = 8 k = 8 k = 8
不妨设 f i f_i f i i i i 1 1 1
考虑进行几次 2 操作再进行 1 操作,令 t = ⌊ log 2 i ⌋ t = \lfloor \log_2 i \rfloor t = ⌊ log 2 i ⌋
f i = 1 2 t + 1 ( t + 1 ) + ∑ j = 0 t 1 2 j + 1 ( f i − ( 2 j − 1 ) + 1 + ( j + 1 ) ) f_i = \frac{1}{2^{t + 1}} (t + 1) + \sum_{j = 0}^t \frac{1}{2^{j + 1}} (f_{i - (2^j - 1) + 1} + (j + 1))
f i = 2 t + 1 1 ( t + 1 ) + j = 0 ∑ t 2 j + 1 1 ( f i − ( 2 j − 1 ) + 1 + ( j + 1 ) )
稍微移项成能递推的形式:
f i + 1 = 3 2 f i − 2 − ∑ j = 2 t 1 2 j ( f i − ( 2 j − 1 ) + 1 + ( j + 1 ) ) f_{i + 1} = \frac{3}{2} f_i - 2 - \sum_{j = 2}^t \frac{1}{2^j} (f_{i - (2^j - 1) + 1} + (j + 1))
f i + 1 = 2 3 f i − 2 − j = 2 ∑ t 2 j 1 ( f i − ( 2 j − 1 ) + 1 + ( j + 1 ) )
然后发现所有元都可以写成 a f 1 + b a f_1 + b a f 1 + b f 2 n f_{2n} f 2 n f 1 f_1 f 1
这 b 题卡常,得上个快速取模.
若不存在两个相同的元素,则不存在解,否则直接选择两个相同的元素即可.
先考虑怎么求 f f f f l , r = f ( S [ l , r ] ) f_{l, r} = f(S[l, r]) f l , r = f ( S [ l , r ] )
若 S l S_l S l f l , r = f l + 1 , r f_{l, r} = f_{l + 1, r} f l , r = f l + 1 , r S r S_r S r k k k f l , r ← f l + 1 , k − 1 × f k + 1 , r f_{l, r} \leftarrow f_{l + 1, k - 1} \times f_{k + 1, r} f l , r ← f l + 1 , k − 1 × f k + 1 , r
然后发现 f f f f m o d 998244353 f \bmod 998244353 f m o d 9 9 8 2 4 4 3 5 3 f m o d 2 32 f \bmod 2^{32} f m o d 2 3 2 p p p q q q l ⊕ r ⊕ f l , r ≡ ( p l , r − q l , r ) + q l , r ⊕ l ⊕ r ( m o d 998244353 ) l \oplus r \oplus f_{l, r} \equiv (p_{l, r} - q_{l, r}) + q_{l, r} \oplus l \oplus r \pmod {998244353} l ⊕ r ⊕ f l , r ≡ ( p l , r − q l , r ) + q l , r ⊕ l ⊕ r ( m o d 9 9 8 2 4 4 3 5 3 )
问题实际上是要我们最大化缩完点后的图的大小.
若 u u u
由于缩点操作不能缩掉环,且一个长为 s s s t t t t ∣ s t | s t ∣ s gcd \gcd g cd
若不存在环,则每个连通块都是有向链,直接将所有链首尾相连就是答案.
没写代码. \Huge\color{red}\text{没写代码.} 没写代码.
令 n u m l , r \mathrm{num}_{l, r} n u m l , r [ l , r ] [l, r] [ l , r ] len ( x ) \operatorname{len}(x) l e n ( x ) x x x ⌊ lg x ⌋ + 1 \lfloor \lg x \rfloor + 1 ⌊ lg x ⌋ + 1
先考虑找到最小的 b k b_k b k b k b_k b k f i f_i f i j j j [ j , i ] [j, i] [ j , i ]
i + 1 → f j , j > i ∧ n u m f i , i < n u m i + 1 , j i + 1 \to f_j, j > i \land \mathrm{num}_{f_i, i} < \mathrm{num}_{i + 1, j}
i + 1 → f j , j > i ∧ n u m f i , i < n u m i + 1 , j
再考虑最大化字典序,设 g i g_i g i j j j [ g i , j ] [g_i, j] [ g i , j ]
i − 1 → g j , j < i ∧ n u m j , i − 1 < n u m i , g i i - 1 \to g_j, j < i \land \mathrm{num}_{j, i - 1} < \mathrm{num}_{i, g_i}
i − 1 → g j , j < i ∧ n u m j , i − 1 < n u m i , g i
都可以通过二分 LCP 优化!
min { b , n } + min { g , n } − n + 1 \min\{b, n\} + \min\{g, n\} - n + 1
min { b , n } + min { g , n } − n + 1
首先可以一眼一个 DP,记 a n c u \mathrm{anc}_u a n c u u u u d e p u \mathrm{dep}_u d e p u u u u f u f_u f u u u u
f u = min v ∈ a n c u { f v + ( d e p u − d e p v ) a u + b u } = min v ∈ a n c u { f v − d e p v a u } + d e p u a u + b u f_u = \min_{v \in \mathrm{anc}_u} \{f_v + (\mathrm{dep}_u - \mathrm{dep}_v)a_u + b_u\} = \min_{v \in \mathrm{anc}_u} \{f_v - \mathrm{dep}_v a_u\} + \mathrm{dep}_u a_u + b_u
f u = v ∈ a n c u min { f v + ( d e p u − d e p v ) a u + b u } = v ∈ a n c u min { f v − d e p v a u } + d e p u a u + b u
显然这玩意可以斜率优化,由于祖先链上的点的 d e p \mathrm{dep} d e p a u a_u a u
若局面已经确定,首先有个典中典 DP:设 f i , j f_{i, j} f i , j i i i j j j f i , j = max { f i , j − 1 , f i , j , f i , j + 1 } + a i , j f_{i, j} = \max\{f_{i, j - 1}, f_{i, j}, f_{i, j + 1}\} + a_{i, j} f i , j = max { f i , j − 1 , f i , j , f i , j + 1 } + a i , j a i , j a_{i, j} a i , j i i i j j j
打表发现,这个 DP 第二维任意两个元素的差不超过 5 5 5 1 1 1
首先在最优策略下,手上不可能有多于 1 0 6 10^6 1 0 6 1 0 6 10^6 1 0 6
若最终局面确定,则交换次数就是排列的逆序对数.
那么设 f i , j , k , 0 / 1 / 2 f_{i, j, k, 0 / 1 / 2} f i , j , k , 0 / 1 / 2 i i i j j j k k k
太困难!!!
A124197 .
然而不能直接算,查 FORMULA 发现计算式为:
1 + n + ∑ i = 1 n − 1 ∑ j = 1 i ∑ d ∣ j [ d m o d 2 = 1 ] 1 + n + \sum_{i = 1}^{n - 1} \sum_{j = 1}^i \sum_{d | j} [d \bmod 2 = 1]
1 + n + i = 1 ∑ n − 1 j = 1 ∑ i d ∣ j ∑ [ d m o d 2 = 1 ]
继续查表发现若令
f i = ∑ j = 1 i d ( i ) = ∑ j = 1 i ⌊ i / j ⌋ f_i = \sum_{j = 1}^i d(i) = \sum_{j = 1}^i \lfloor i / j \rfloor
f i = j = 1 ∑ i d ( i ) = j = 1 ∑ i ⌊ i / j ⌋
那么有
原式 = 1 + n + ∑ i = 1 n − 1 f i − f ⌊ i / 2 ⌋ \text{原式} = 1 + n + \sum_{i = 1}^{n - 1} f_i - f_{\lfloor i / 2 \rfloor}
原式 = 1 + n + i = 1 ∑ n − 1 f i − f ⌊ i / 2 ⌋
不妨令
g n = ∑ i = 1 n f i − f ⌊ i / 2 ⌋ g_n = \sum_{i = 1}^{n} f_i - f_{\lfloor i / 2 \rfloor}
g n = i = 1 ∑ n f i − f ⌊ i / 2 ⌋
容易发现若令
h n = ∑ i = 1 n ∑ j = 1 i ⌊ i / j ⌋ h_n = \sum_{i = 1}^n \sum_{j = 1}^i \lfloor i / j \rfloor
h n = i = 1 ∑ n j = 1 ∑ i ⌊ i / j ⌋
那么有
g n = h n − h ⌊ n / 2 ⌋ − h ⌊ ( n − 1 ) / 2 ⌋ g_n = h_n - h_{\lfloor n / 2 \rfloor} - h_{\lfloor (n - 1) / 2 \rfloor}
g n = h n − h ⌊ n / 2 ⌋ − h ⌊ ( n − 1 ) / 2 ⌋
只需解决 h h h
h n = ∑ i = 1 n ∑ j = 1 i ⌊ i / j ⌋ = ∑ j = 1 n ∑ i = j n ⌊ i / j ⌋ h_n = \sum_{i = 1}^n \sum_{j = 1}^i \lfloor i / j \rfloor = \sum_{j = 1}^n \sum_{i = j}^n \lfloor i / j \rfloor
h n = i = 1 ∑ n j = 1 ∑ i ⌊ i / j ⌋ = j = 1 ∑ n i = j ∑ n ⌊ i / j ⌋
然后对于一个 j j j k j ≤ i < ( k + 1 ) j kj \le i < (k + 1)j k j ≤ i < ( k + 1 ) j ⌊ i / j ⌋ = k \lfloor i / j \rfloor = k ⌊ i / j ⌋ = k
h n = ∑ j = 1 n j 1 2 ( 1 + ⌊ n − j + 1 j ⌋ ) ⌊ n − j + 1 j ⌋ + ( ( n − j + 1 ) m o d j ) ( ⌊ n − j + 1 j ⌋ + 1 ) h_n = \sum_{j = 1}^n j \frac{1}{2} \left(1 + \left\lfloor \frac{n - j + 1}{j} \right\rfloor\right) \left\lfloor \frac{n - j + 1}{j} \right\rfloor + ((n - j + 1) \bmod j)\left(\left\lfloor \frac{n - j + 1}{j} \right\rfloor + 1\right)
h n = j = 1 ∑ n j 2 1 ( 1 + ⌊ j n − j + 1 ⌋ ) ⌊ j n − j + 1 ⌋ + ( ( n − j + 1 ) m o d j ) ( ⌊ j n − j + 1 ⌋ + 1 )
然后就可以整除分块 O ( n ) O(\sqrt{n}) O ( n )
i i i 1 , 2 , 3 1,2,3 1 , 2 , 3 0 , 1 , 2 , 3 0,1,2,3 0 , 1 , 2 , 3
垃圾做法.
首先,如果我们确定了一首歌最终听的次数,我们肯定会在第一次到这首歌的时候听完.
于是我们可以设计一个 DP,计算出从 1 1 1 i i i f i , j f_{i, j} f i , j i i i j j j
f i , j = max k { f i − 1 , k + 1 2 ( a i + a i − ( j − k − 2 ) b i ) ( j − k − 1 ) } f_{i, j} = \max_k\left\{f_{i - 1, k} + \frac{1}{2}(a_i + a_i - (j - k - 2)b_i)(j - k - 1)\right\}
f i , j = k max { f i − 1 , k + 2 1 ( a i + a i − ( j − k − 2 ) b i ) ( j − k − 1 ) }
显然可以斜率优化.
然后最终的路径一定是往某个方向走一段之后回到 1 1 1
注意两个路径不要有重叠.
满足条件的 d d d 3-smooth 数 ,故只用凑 2 2 2 3 3 3
1 0 9 10^9 1 0 9 这篇博客 大概只有 300 300 3 0 0
太困难!!!
典.
典.
为什么我总在写垃圾题啊?
考查修改一个位置的值会对哪些 c c c l i m i \mathrm{lim}_i l i m i [ 1 , i ] [1, i] [ 1 , i ] b i b_i b i n x t i \mathrm{nxt}_i n x t i [ 1 , i ] [1, i] [ 1 , i ] b i + 1 b_i + 1 b i + 1 a i a_i a i v v v j ≥ i j \ge i j ≥ i c j c_j c j
a i ≥ l i m j , v ≥ l i m j a_i \ge \mathrm{lim}_j, v \ge \mathrm{lim}_j a i ≥ l i m j , v ≥ l i m j v − a i v - a_i v − a i
a i ≥ l i m j , v < l i m j a_i \ge \mathrm{lim}_j, v < \mathrm{lim}_j a i ≥ l i m j , v < l i m j v v v n x t j \mathrm{nxt}_j n x t j
v ≥ n x t j v \ge \mathrm{nxt}_j v ≥ n x t j v − a i v - a_i v − a i v < n x t j v < \mathrm{nxt}_j v < n x t j n x t j − a i \mathrm{nxt}_j - a_i n x t j − a i
a i < l i m j , v ≥ l i m j a_i < \mathrm{lim}_j, v \ge \mathrm{lim}_j a i < l i m j , v ≥ l i m j v − l i m j v - \mathrm{lim}_j v − l i m j
a i < l i m j , v < l i m j a_i < \mathrm{lim}_j, v < \mathrm{lim}_j a i < l i m j , v < l i m j 0 0 0
倒着扫一边处理询问即可,注意需要支持动态二维数点,我使用了树状数组套动态开点线段树.
原题是 AGC006D .
带上区间查询就再二分一下距离中间最近的相邻两个相同的位置,这个可以用 ST 表维护区间相邻两个数的最大值的最小值.