10 月模拟赛记录

发表于 2023-11-02 分类于做题记录

2023.10.17

100 + 40 + 0 + 40．

爱来自【数据删除】．

A. 最大公约数

维护可选的因数，查询直接枚举当前数字的因数，然后把新产生的因数打标记即可．

B. 子序列

钦定每次删除一个连续段的最后一个字符，容易发现这样的删除序列和题意中的序列构成双射．

考虑区间 DP，设 $f_{l, r}$ 表示删空区间 $[l, r]$ 的方案数，转移枚举上一次删除的位置 $k$ ，满足 $a_k \not= a_{r + 1}$ ，这样两边方案独立，乘起来再乘个组合数即可．

C. 最短路

太困难！！！

D. 树

不妨设 $f_u$ 表示以 $u$ 为根的子树， $u$ 所在的连通块的大小．设 $w(u, v)$ 代表 $(u, v)$ 这条边的权值，白色为 $0$ ，黑色为 $1$ ．有转移 $f_u = 1 + \sum_v c(u, v) f_v$ ．带修可以用动态 DP 技巧维护．

然后查询需要跳到当前所在联通块的最高点查询，这个容易通过重链剖分加线段树实现．

2023.10.18

100 + 100 + 0 + 0．

爱来自温州中学．

A. 买邮票

设 $f_{i, j}$ 表示考虑了前 $i$ 个位置，选了 $j$ 个套装，能获得最多的邮票数．显然对于右端点相同的所有区间，选择左端点最小的那个是最优的．然后转移枚举上一个选取的右端点在哪，分类讨论是否再当前区间的左端点右边即可 $O(n)$ 转移，再上个树状数组优化即可通过．

B. 数颜色

按题意分讨即可．

C. 树上问题

问题实际上是将边集划分成若干条路径 $u \to v$ ，最小化 $\sum C_u C_v$ ．

考虑一个类似线头 DP 的东西，设 $f_{u, l}$ 表示考虑了 $u$ 子树的方案，线头的另一端为叶子 $l$ 的最小代价（即钦定 $l$ 和 $u$ 的某个祖先相连）．转移考虑从哪个子树拉线头上来，剩余子树中的线头都要接到 $u$ 上，于是我们有转移

f_{u, l} = \min_v\left\{f_{v, l} + \sum_{w \not= v} \min_{r} \{f_{w, r} + C_uC_r\} \right\}

对于 $u$ 子树中的一个叶子节点 $l$ ，考虑一条直线 $y = C_l x + f_{u, l}$ ，转移时只会用到这些直线的下凸壳，且转移只会改变直线截距，使用李超树合并即可．

D. 字符串

Manacher 可以给出某些字符相等的信息，我们先将这些点缩起来．

对于每个位置，其回文半径外的第一个位置对应的两个字符一定不等，可以通过比对 $\mathrm{rk}$ 数组来得到大小关系．

考虑 $\mathrm{rk}_{\mathrm{sa}_{i - 1}}$ 和 $\mathrm{rk}_{\mathrm{sa}_{i}}$ 的大小，若前者大于后者，则可以确定 $\mathrm{sa}_{i - 1}$ 位置的字符小于 $\mathrm{sa}_{i}$ 位置的字符，反之则可能等于．

考虑对已知的大小关系建边，这张图包含了所有已知的偏序关系．缩点后 DP 出每个点的下界，就能构造字符串．

2023.10.24

50 + 70 + 20 + 0．

爱来自大连二十四中．

A. 推数机

容易发现经过 $\ge 2$ 次操作，可以凑出任意只含输入中出现过的数位的三位数．

分 $n = 1$ 和其他情况，直接计数即可．注意多测组数．

B. 三元组

巨大分讨题．狗都不补．

C. 徽章

由于 $\sum m \le n$ ，故对 $m$ 根号分治．

对于 $m > \sqrt{n}$ 的部分，询问个数不超过 $\sqrt{n}$ 个，每次直接暴力做，这一部分的复杂度是 $O(n \sqrt{n})$ ．

对于 $m < \sqrt{n}$ 的部分，考虑每次单点加操作能够对哪些区间造成贡献．若对位置 $x$ 进行单点加，所有满足 $l_i < x$ 且 $x < r_i$ 的区间 $i$ 的和都会加 $1$ ，贡献情况取反．若将区间 $[l_i, r_i]$ 视作二维平面上的点 $(l_i, r_i)$ ，对于一组询问 $x_1, x_2, \cdots, x_m$ ，下图中黄色矩形中的点代表的区间会计入答案：

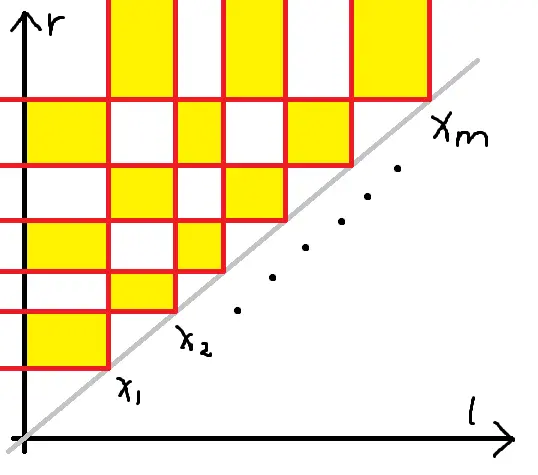
爱来自 mspaint

对于一组询问，会产生 $m^2$ 个矩形查询，又由于 $m < \sqrt{n}$ ，所以有 $\sum m^2 \le n\sqrt{n}$ ．直接将所有矩形询问离线下来扫描线，内层使用分块平衡复杂度，即可做到时空复杂度 $O(n \sqrt{n})$ ．

然而根号空间太不牛了！考虑怎么线性空间．发现 $x_i$ 会和所有 $j \ge i$ 的 $x_j$ 产生一组矩形询问，故不必将某个 $x_i$ 产生的所有询问记录下来，记录 $i$ 即可．空间复杂度 $O(n)$ ．

D. 网格

先给 $n$ 和 $m$ 减 $1$ ．

考虑计算边上恰好具有 $i + 1$ 个整点的边数．我们可以钦定边上 $\frac{1}{k}$ 处为整点，这样的方案数是好统计的．然后会多算整点个数是 $i$ 的整数倍加一的边，减去即可．若设边上恰好有 $i + 1$ 的整点的边数为 $f_i$ ，有：

\begin{aligned} f_i = & (m + 1) \sum_{i | k}^n (n - k + 1) + (n + 1) \sum_{i | k}^m (m - k + 1) \\ &+ 2 \sum_{i | k}^n (n - k + 1) \sum_{i | k}^m (m - k + 1) - \sum_{i | k, i \not= k} f_k \end{aligned}

然后考虑先算出任意三点构成的图形的边上整点数的和，再减去不构成三角形时的整点数．

计算前者可以考虑枚举第三个点．注意第三个点取端点时这条边贡献两次，故第一部分为：

\sum_i ((n + 1)(m + 1) + 2) \times f_i \times i

不构成三角形时三点共线，我们将每个不构成三角形的图形的贡献放在最长边上统计．枚举每种边作为最长边，第二部分为：

\sum_i (i + 1) \times f_i \times 2i

相减即可．复杂度 $O(n \log n)$ ．

2023.10.26

50 + 50 + 50 + 50．鉴定为唐．

爱来自厦门一中．

A. 孔圣临川

要么 std 挂了要么题面挂了．不写了．

B. 桑榆非晚

注意到每个子树是否选取只和子树大小和根的父边边权相关，而由于树随机生成，边权 $\le 5$ ，故本质不同的物品只有 $O(\sqrt{n})$ 种．弄个单调队列优化多重背包即可．

C. 渔夫知世

$\Huge\color{red}\text{没写代码．}$

首先可以发现，最优解中不存在区间合并的情况，也就是说一定是从一个点开始一路合并．

然后不会了！然后有结论，最优解一定是不断合并一边直到 $\gcd$ 改变，然后再往某个方向合并．

又每次 $\gcd$ 改变至少除 $2$ ，这样的点数只有 $O(n \log n)$ 个，求出来 DP 即可．

D. 离合不骚

看不懂题解啊．

2023.10.28

0 + 20 + 0 + 0．都给我唐完了．

爱来自焦作一中．

A. 机械之心

设有最多空格子的行或列中，空格子的个数为 $x$ ，显然答案有下界 $x$ ．接下来给出一种能够达到这个下界的构造：按照任意顺序考虑空格子，设当前空格子为 $(i, j)$ ，然后 $i$ 行第一个没被填过的数为 $x$ ， $j$ 列第一个没被填过的数为 $y$ ．若 $x = y$ ，那么直接填入即可，否则令 $x < y$ ，我们直接填入 $x$ ，但是这一列已经存在 $x$ 了，我们将那个 $x$ 换成 $y$ ，然后那一行可能也存在 $y$ ，做类似调整即可．

为啥对呢，不懂啊．

B. 同归世界

$\Huge\color{red}\text{没写代码．}$

容易发现，题目中给的树是 Cartesian 树，于是考虑求出一个数在 Cartesian 树上的对应区间 $l_i, r_i$ ， $\sum (r_i - l_i + 1)b_i$ 即为一个区间的答案．

然后需要有一个观察：设 $[l_i, r_i]$ 表示原序列上 $i$ 位置对应的区间，那么对于区间 $[L, R]$ 的 Cartesian 树，其对应区间为 $[\max\{l_i, L\}, \min\{r_i, R\}]$ ．

询问 1 可以差分成 4 个询问 2，故只用解决询问 2 即可．

设询问区间为 $[L, R]$ ，则答案为

\sum_{p = L}^R \sum_{q = p}^R \sum_{i = p}^q (\min\{r_i, q\} - \max\{l_i, p\} +1) b_i

拆成三部分

\sum_{p = L}^R \sum_{q = p}^R \sum_{i = p}^q b_i \min\{r_i, q\} - \sum_{p = L}^R \sum_{q = p}^R \sum_{i = p}^q b_i \max\{l_i, p\} + \sum_{p = L}^R \sum_{q = p}^R \sum_{i = p}^q b_i

第三部分是经典的，做 $b_i$ ， $i b_i$ ， $i^2 b_i$ 的前缀和即可 $O(1)$ 查询．考虑怎么做前两部分．

先拆第一部分的式子：

\begin{alignedat}{} & & & \sum_{p = L}^R \sum_{q = p}^R \sum_{i = p}^q b_i \min\{r_i, q\} \\ & = & & \sum_{i = L}^R b_i \sum_{p = L}^i \sum_{q = i}^R \min\{r_i, q\} \\ & = & & \sum_{i = L}^R b_i (i - L + 1) \sum_{q = i}^R \min\{r_i, q\} \\ & = & & \begin{alignedat}{} & & & \sum_{i = L}^R [r_i \le R] b_i (i - L + 1) \left(\frac{1}{2} (i + r_i)(r_i - i + 1) + r_i(R - r_i)\right) \\ & + & & \sum_{i = L}^R [r_i > R] b_i (i - L + 1) \left(\frac{1}{2} (i + R)(R - i + 1)\right) \end{alignedat} \\ & = & & \begin{alignedat}{} & & & \sum_{i = L}^R [r_i \le R] \left(-\frac{1}{2} i^3 b_i + \left(\frac{1}{2} - \frac{L}{2}\right) i b_i + \frac{L}{2} i^2 b_i + \left(\frac{1}{2} + R\right) i b_i r_i + \left(\frac{1}{2} - \frac{L}{2} + R - LR\right) b_i r_i - \frac{1}{2} i b_i {r_i}^2 + \left(-\frac{1}{2} + \frac{L}{2}\right) b_i {r_i}^2\right) \\ & + & & \sum_{i = L}^R [r_i > R] \left(-\frac{1}{2} i^3 b_i + \frac{L}{2} i^2 b_i + \left(\frac{1}{2} - \frac{L}{2} + \frac{R}{2} + \frac{R^2}{2}\right) i b_i + \left(\frac{R}{2} - \frac{LR}{2} + \frac{R^2}{2} - \frac{LR^2}{2}\right) b_i\right) \end{alignedat} \\ \end{alignedat}

再拆第二部分的式子：

\begin{alignedat}{} & & & \sum_{p = L}^R \sum_{q = p}^R \sum_{i = p}^q b_i \max\{l_i, p\} \\ & = & & \begin{alignedat}{} & & & \sum_{i = L}^R [l_i \le L] b_i (R - i + 1) \left(\frac{1}{2} (i + L)(L - i + 1)\right) \\ & + & & \sum_{i = L}^R [l_i > L] b_i (i - L + 1) \left(\frac{1}{2} (l_i + i)(i - l_i + 1) + l_i(l_i - L)\right) \end{alignedat} \\ & = & & \begin{alignedat}{} & & & \sum_{i = L}^R [l_i \le L] \left(-\frac{1}{2} i^3 b_i + \left(\frac{1}{2} - \frac{L}{2} +\frac{L^2}{2} + \frac{R}{2}\right) i b_i + \frac{R}{2} i^2 b_i + \left(\frac{L}{2} - \frac{L^2}{2} + \frac{LR}{2} - \frac{L^2R}{2}\right) b_i\right) \\ & + & & \sum_{i = L}^R [l_i > L] \left(-\frac{1}{2} i^3 b_i + \left(\frac{1}{2} + \frac{R}{2}\right) i b_i + \frac{R}{2} i^2 b_i + \left(-\frac{1}{2} + L\right) i b_i l_i + \left(\frac{1}{2} - L + \frac{R}{2} - LR\right) b_i l_i - \frac{1}{2} i b_i {l_i}^2 + \left(\frac{1}{2} + \frac{R}{2}\right) b_i {l_i}^2\right) \end{alignedat} \end{alignedat}

全都塞进偏序里维护即可．

C. 积云四月

太困难！！！

D. 仲夏晚风

太困难！！！

2023.10.30

40 + 4 + 0 + 8．

爱来自郑州外国语学校．

A. 01 串

知道前 $k$ 个的值可以推出整个序列该如何填，所以只需对前 $k$ 个的填写方案计数即可．

考虑逐个计算前 $k$ 个位置中有哪些位置可以随便填，设正在计算 $i$ ，不妨假设 $i$ 填 $0$ ，然后在递推和 $i$ 模 $k$ 同余的位置填写什么的过程中计算填过的最大值和最小值，若相差 $\ge 2$ ，那么不存在方案，若相差为 $1$ 则方案确定，否则就可以随便填．然后算出前 $k$ 个要填写几个 $1$ 后直接组合数计算方案即可．

B. 翻转匹配

大分讨题，狗都不补．

C. 建筑修缮

从小到大填，一定不劣．然后我们要考虑的是，对于当前值相同的元素，以何种方式将其全体加一是最优秀的．

不难想到可以先给最靠左和最靠右的元素加一，剩下的使用这两个抬升，这样做是最优的．需要分讨先抬最靠左的还是最靠右的．

模拟这个过程可以使用一个 std::set 来维护当前所有需要抬升的位置，配合线段树维护区间最值，当每个点被插入 set 中时，将其从线段树中去掉，就可以查询大于自己的最小值．注意操作前去掉已经到达目标值的元素．

D. 旅行商问题

太困难！！！

2023.11.1

100 + 100 + 30 + 10．

爱来自余姚中学．

A. 原子

考虑对于所有 $j > i$ ，建边 $i \to j$ ．假设从点 $i$ 之前的点出发的边已经全都被覆盖完，点 $i$ 至少需要 $n - i$ 个在该点的氢原子才能取完从他出发的所有边，若设 $c_i$ 为 $1$ 到 $i$ 的路径数，那么此时点 $i$ 上已经有 $c_i$ 个氢原子，可以重复利用．按照上述描述直接构造即可．

我也不知道为什么是对的．貌似可以用 Dilworth 定理证明．

B. 旅行计划

考虑对一条边 $(u, v)$ ，我们可以进行哪些操作：

若数目为偶数，那么可以拿完这条边，并能拿连向的点的子树．
若数目为大于 $1$ 的奇数，那么可以舍弃一条当偶数边用，也可以死在这一子树中．
若重边只有一条，要么不拿连向的子树，要么死在那一子树中．

现在可以设计树形 DP 了！设 $f_{u, 0 / 1}$ 表示考虑了 $u$ 的子树，回到 / 不回到 $u$ ，能够拿的最大边数，转移按照上述操作分讨即可．然后再换个根就能够通过本题．

C. 禁止套娃

抄的 pdf．/cf

求本质不同的子序列有一个经典 DP，就是只在其第一次出现时统计贡献（即贪心匹配）．设 $i$ 为以 $i$ 结尾的本质不同子序列数目，设 $a_i$ 上一次出现的位置是 $p_i$ ，那么有

f_i = \sum_{j = p_i}^{i - 1} f_j

现在套起来了，该如何是好呢？尝试观察一下选择的性质，设外层选择的下标序列为 $p_i$ ，内层选择的下标序列为 $q_i$ ，显然 $p_i$ 是 $q_i$ 的一个子序列，为了满足贪心匹配的规则，需要有：

对于所有 $i$ ，不存在 $j$ 满足 $p_{i - 1} < j < p_i$ 且 $a_j = a_{p_i}$ ．
对于所有 $i$ ，不存在 $j$ 满足 $q_{i - 1} < p_j < q_i$ 且 $a_{p_j} = a_{q_i}$ ．

尝试对 $q$ DP．设 $f_i$ 表示考虑了 $i$ 以前的元素， $q$ 选择了 $i$ 的方案数．转移枚举上一个 $q$ 选了什么，若要从 $f_j$ 转移，则需计算 $[j + 1, i - 1]$ 选择 $a$ 的方案数，使得选择出来的 $a$ 满足贪心匹配规则．设区间中被 $a$ 选择的下标序列为 $r$ ，那么有如下限制：

对于所有 $i$ ，不存在 $j$ 满足 $r_{i - 1} < j < r_i$ 且 $a_j = a_{r_i}$ ．
对于 $r$ 中最后一个元素 $x$ ，不存在 $j$ 满足 $x < j < i$ 且 $a_j = a_i$ ．
对于所有 $i$ ， $r_i \not= a_i$ ．

考虑 DP 出这个系数，设 $g_{i, j}$ 表示 $[j, i]$ 这一区间，满足 1 和 3 条件的选取方案，转移时记录这个数上一次出现时的位置，弄个和原始 DP 差不多的差分操作就行了．

D. 简单题

太困难！！！